今回は場合の数の解き方・考え方について解説していこうと思います。
結論から言うと、中学受験の基本を学ぶ段階では樹形図を重視します。
場合の数を苦手としている子は本当に多いです。
その原因の一つは、場合の数が中学受験の全単元の中でもトップクラスに「モノが見えない」からだと思います。
旅人算であれば人が動いているという映像がイメージしやすいですし、図形であれば実物が問題に書いてありますからイメージが楽です。
しかし場合の数という単元は、~通りという計算上の数字を扱う分野のため、自分が何をやっているのか分からなくなり、中学受験生が苦手としてしまいがちです。
場合の数をみえるようにする解き方のツールが樹形図です。
以前別記事で子供の認知特性についてお話ししました。
子供の認知の特性について。視覚優位・聴覚優位・言語優位
場合の数で何をやっているのか理解し辛いという子に解き方を指導する際には、初めは全ての問題を樹形図を使った解法で解説します。
つまり書き出しです。
場合の数の問題というのは、気合と根性で書きだしていけば答えを出せる問題が多いです。時間が無限にあれば計算などしなくても、ひたすら樹形図を書いていく解法で答えは出せます。
順列であっても組み合わせであっても、基本的に最初は樹形図で説明します。
もちろん入試本番で樹形図を書いていては時間が足りなくなります。
計算で求める方法に関連させていきますので、是非最後までお読みください。
まずは「順列」の問題を例に出し、その次に「組み合わせ」の問題を例に出します。「組み合わせ」は、場合の数を学習する上で最初の壁となりやすい所です。
さっそく例題を出してみましょう
問題:A,B,C,D,Eの5人を1列に並べます。並べ方は何通りありますか。
先に答えを書いておくと、120通りです。一般的なテキストの解説には下のような式が載っています。
5×4×3×2×1=120 答え:120
また中学・高校の数学になるとパーミュテーションの記号を使って
5P1=120
のように書かれます。(これは小学生は覚えなくていいです)
さて、ここで「なるほど。5人を並べ替えるときは1~5まで掛け算すればよいのか」では伸びません。
週ごとの確認テストは乗り切れるでしょうが、入試に太刀打ちできるだけの知識はつきません。
計算で求める便利な方法は一旦置いておいて、まずは泥臭く樹形図で書き出してみたいと思います。
まずは、一番左にAを置いた場合の樹形図を書きだします。(指導の際にもノートに手書きで同じものを書きます)
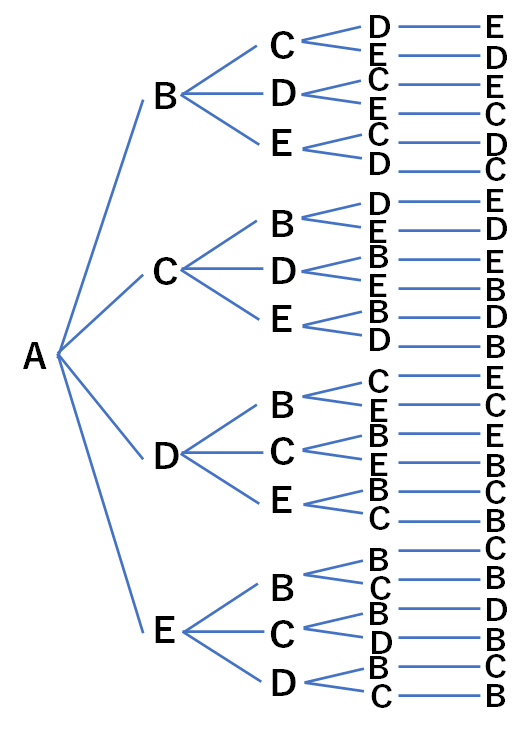
これで、Aから始まるものは全て書き出しましたね。ここまでで24通りです。
さて次に、Bから始まるものも書き出していきましょう。
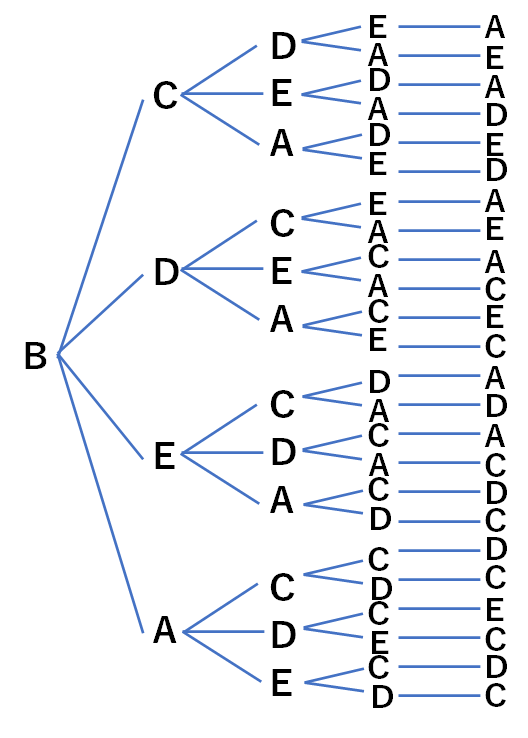
数えてみると、Bから始まるものも24通りですね。(順番がAから昇順になってないのはお許しください。パワーポイントの置き換え機能を使って複製したという裏話が……)
では次に、Cから始まるものも……
とこの辺りまでやったところで、大体いつも生徒から「先生、もういいじゃん!掛け算しようよ」
のように提案してくれます。ふぅ、助かりました。
この気づきが場合の数の本質です。
計算方法を教えてよりも、面倒だから楽したい!という切実な気持ちから湧き上がる解法の方が定着しますし、応用問題にも進みやすくなります。
まぁ一応全通り作りましたので、まとめた画像を貼っておきます。
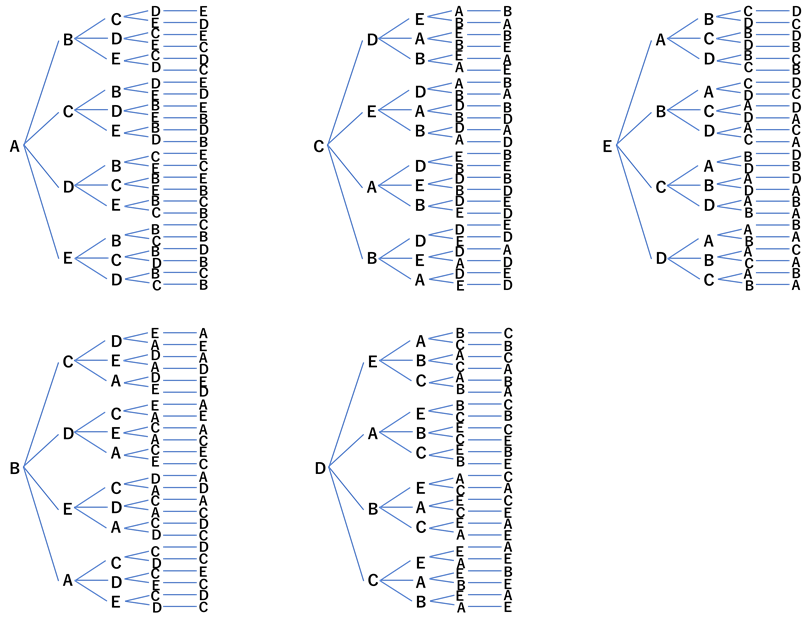
こんなわけで、答えは120通りです。(順番がAから昇順になっていないのは許してください……)
さて、これを全部樹形図で書き出して解く人は実際にはいないですよね。
24×5=120 と計算するはずです。
では次に、この「24」の部分も計算で求められないか考えていきましょう。
下の図を見てみてください。
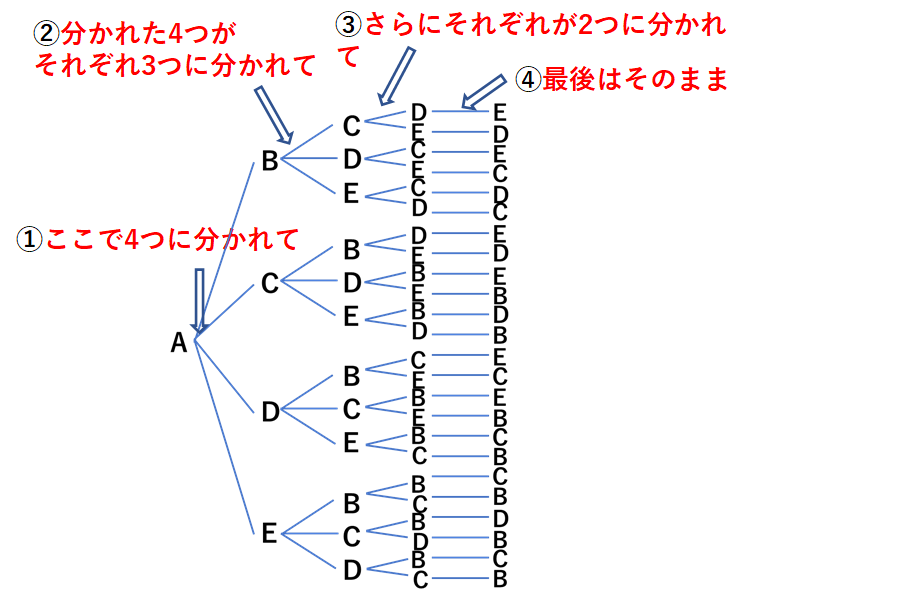
樹形図はまずAから4本の線に枝分かれしています。
次に、枝分かれした4本の線がそれぞれ3本に枝分かれしています。
さらにそのそれぞれが2本に枝分かれしていて
最後は枝分かれせずそのままです。
これを式で表すと
4×3×2×1
になりますね。24通りです。
これに5を書ければOKです。なぜなら、最初の一個目をAにするかBにするか、C,D,Eと5通りの選択肢があるからです。
ですから
5×4×3×2×1=120
という式になります。
これが「5から1まで掛け算する」という公式の意味です。
解説はここまでです!最後まで読んでくださりありがとうございます。
ちなみに「4つに枝分かれして、その先にが3つに枝分かれして……」という状況を「4×3×2×1」という式に変換することが直感的に理解できない子も居ます。
そうした子には追加で別のアプローチから理解の醸成を目指します。その方法はまた別の機会に。
数学が得意な保護者の方であれば「何をそんな当たり前のことを」と思われる解説だったかもしれませんが、場合の数を習いたての子はこの辺りの発想が抜けていることが多いです。
塾の先生が良い先生であれば教えてもらっているかもしれませんが、ここまでの内容は定着していない子も多いです。
樹形図は大手塾の多くは小学4年生で習うのですが、小5・小6で本格的に場合の数が導入された際に、樹形図とのつながりがきちんと解説されていないケースもあるようです。
ぜひお子様がこの辺りのことを理解できているのか、確認してみてください。
さて、次に組み合わせの場合ですが……これは次の記事に持ち越しましょう。
テーマは「6で割るってどういうこと?」です。ご期待ください。
今回からしばらく、場合の数に関する投稿を続けていきます。ご期待ください。
場合の数に関する関連記事はこちら
関連記事①:中学受験の場合の数・道順の基本全パターン攻略!書き出す解き方と計算で求める解き方と
(道順の問題にはいくつかのパターンがあります。全パターンを網羅的に解説しました)
関連記事②:aaabbcの並び替え・重複順列・同じものを含む順列の解き方・計算方法~割る意味が目で見て一発で分かるように
(多くの受験生がなんとなくの理解のままにして、暗記で乗り切ろうとしてしまう「同じものを含む順列」の割る意味を基礎から解説しました)
さて、いろいろな先生たちが中学受験の指導法をブログで語っています。下のにほんブログ村のリンクから、中学受験の指導法・勉強法ブログのランキングに飛べます。(算田も参加しています。)
どんなブログがあるのか、のぞいてみてはいかが?
にほんブログ村

質問・相談・お仕事の依頼はこちらのメールアドレスへどうぞ
sandasuutarou3.14@gmail.com