中学受験の場合の数で特徴的な出題である道順問題について解説していきます。
道順の問題には大きく分けて２つの解き方があります。
書き出していく解き方と、計算で求める解き方です。

初めのうちは、書き出していく解き方だけ覚えていればOKです。
応用問題まで解けるようになりたい方は計算で求める方法も覚えてください。（道順に限らず中学受験の場合の数は、だいたいどの分野も書き出しと計算の２つの解き方があります。）

最初は基本的な解法から解説し、最後には立体の道順についても解説しますので、是非最後までご覧ください。
今回は真面目な技術論の記事です。

①AからBまで行く道順

次のような問題です。
AからBまで、最短距離で行く行き方は何通りありますか。

この問題は次のように解いていきます。
まず、Aから右と上に一直線の位置に、数字の「1」を書き込んでいきます。

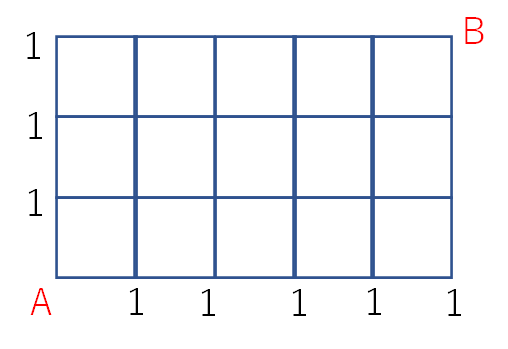
これは、その地点まで行く行き方が1通りだという意味です。
Aからまっすぐ行くしかないので、これらの地点は全て行き方が1通りですね。

次に、各交差点にも数字を書き込んでいきます。
書き込む数字は、その交差点の左と下に書いてある数字の和です。
すると下のような図になります

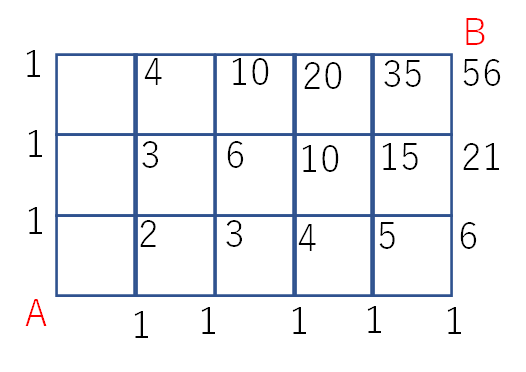
よって、AからBまで行く行き方は56通りとなります。
こちらは基本問題です。
次からバリエーションに分かれていきます。

②Cを通ってAからBまで行く道順

下のような問題です。

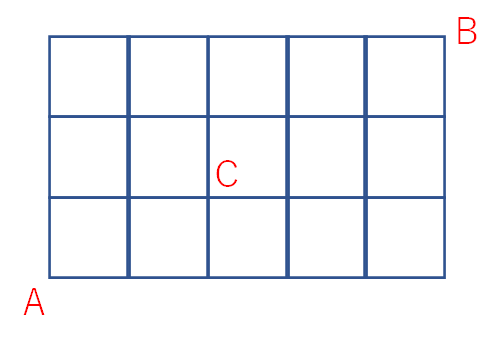
この問題は次のような解き方でやっていきます。
まずは、AからCに行くことだけを考えます。
AからCに行く道順を、先ほどの①と同じ解き方で求めていきます。
下の図のようになります。

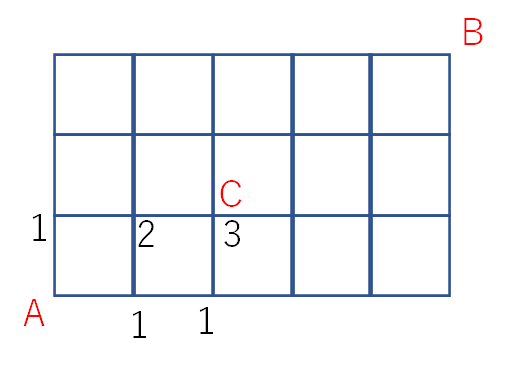
すると、AからとりあえずCまで行く道順は3通りだということが分かりました。
次は、CからBに行くことを考えます。
今までは、出発点から一直線の位置には数字の「1」を書き込んでいましたが、今回はそこが変わります。
Cの時点で既に「3」ですので、下の図のように「3」を書いていきます。
言葉で説明するよりも図を見るのが分かりやすいと思います。

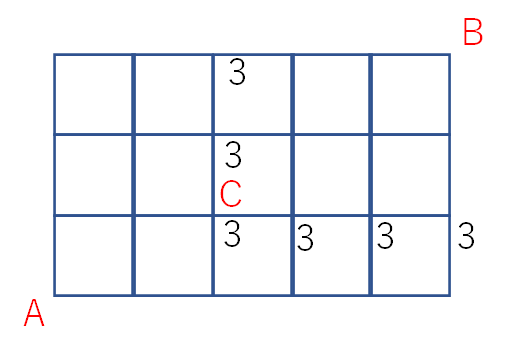
あとは基本問題と同じです。各交差点に、左と下の数字の和を書き込んでいきます。下の図をご覧ください。

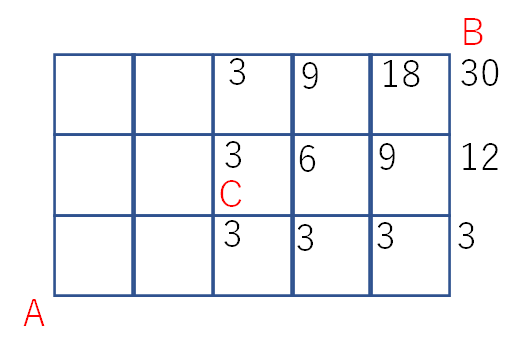
よって答えは30通りとなります。
「〇の点を通って」というパターンの道順はこのような解き方を用います。

③Cを通らずにAからBまで行く道順

 

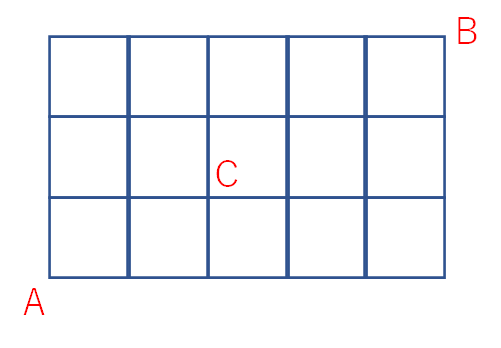
上の図のような図で、AからBまで行く際に、Cを通らずに行く行き方は何通りでしょうか？　という問題です。
（Cの交差点が工事で通行止めになっているような場面設定です。）

では、いつもの解き方と同じく道順を書き出してみます。

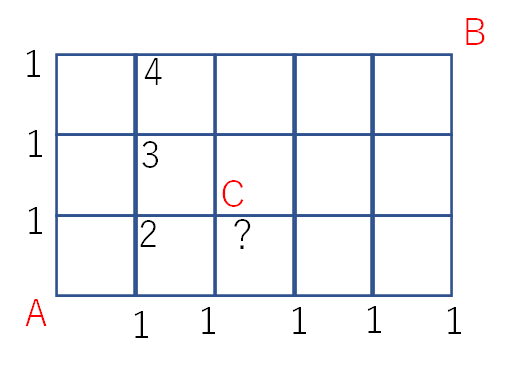
Cの地点はどのようにすればよいのでしょうか。
Cは通行止めですので、数字を書くことは出来ません。バツ印でもつけておきましょうか。

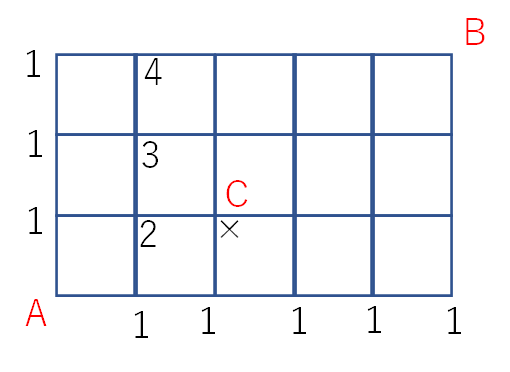
さて、Cの点がバツになったら、その先はどのようになるのでしょうか

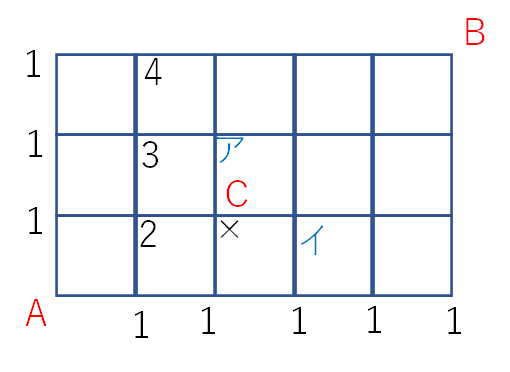
上の図のアとイの地点に書き込む数字を考えます。
まずアを見ます。アの左には「３」が書かれており、下には「×」つまり数字はありません。
ですから、3+0＝3　となり、3を書けば良いです。
同様にイについても考えると、イの左は×、下に１とあるので、イの点も1です。

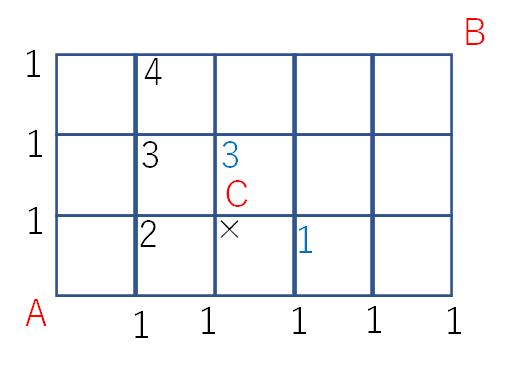
あとは基本と変りません。交差点に数字を書き込んでいくとしたの図のようになり、答えは26通りです。

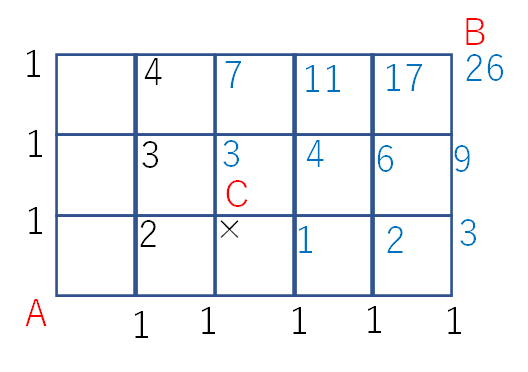
※別解も紹介しておきます。
AからBまでの全通りの行き方から、Cを通る場合を引く事で、Ｃを通らない場合を求める方法です。つまり
56（全通り）-30（Ｃを通る場合）＝26（Ｃ）を通らない場合
です。

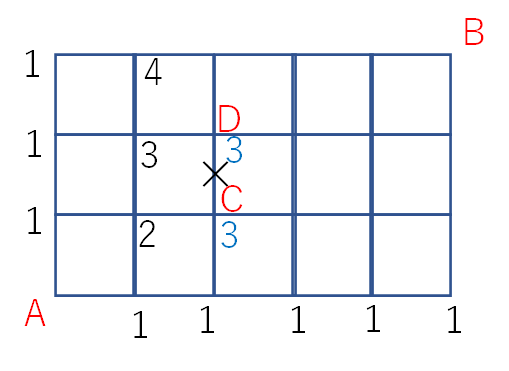
④CからDにつながる道が通行止めの時にAからBまで行く道順

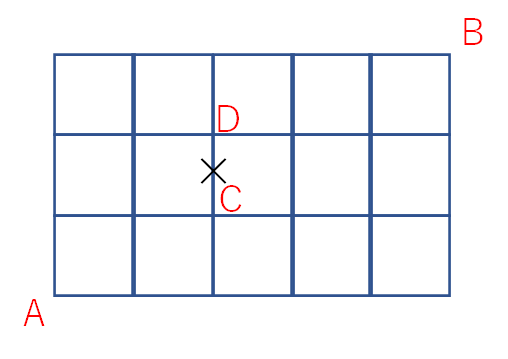
CとDの間の道が通行止めで通れないときに、AからBまで行く行き方は何通りでしょうか？　という問題です。ここまで読んできた方なら、もしかしたら既に想像がついているかもしれません。

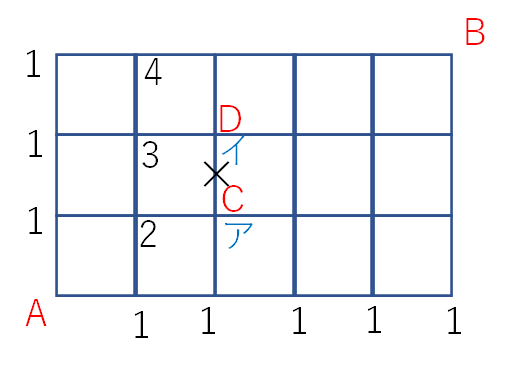
まずはここまでは問題なく書けると思います。
では、アとイにはどのような数字を書き込めば良いのでしょうか。
まずアについて考えます。
Cの点は通ることができます。（通れないのはCとDの間の道だけで、C点は通れます）
C点の左には「２」があり、下には「１」があります。よってアに書き込む数字は2+1＝3　の３となります。これは基本通りですね。

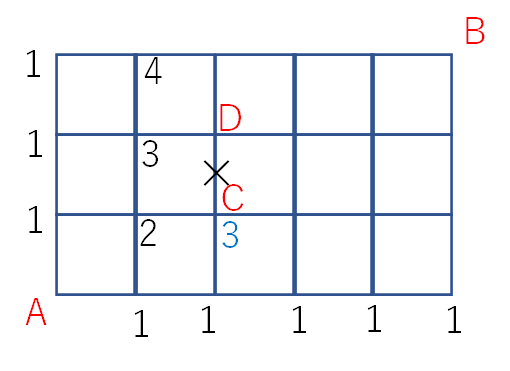
では次にD点に書き込む数字であるイを考えます。
D点の左には「３」と書かれています。Dの下には、「３」と書かれることが先ほど分かりましたが、CとDの間の道は通行止めです。
そのため、Cに書いてある「３」という数字は上に上がることができません。
そのため、イに書かれる数字は3+0＝3　の３となります。

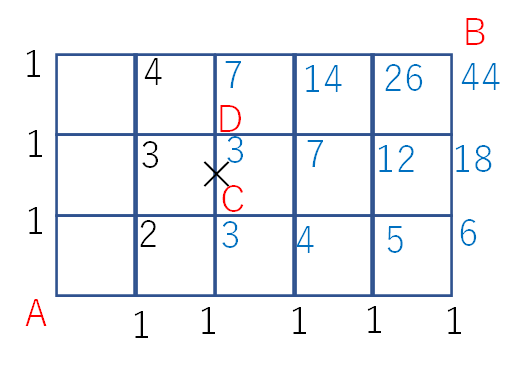
あとはいつも通り書き込んでいくと、答えは44となります。

⑤計算で求める方法

お待たせしました。道順問題を計算で求める方法です。
先に結論から書いておくと「重複順列」の考え方を使います。同じものがある場合の並び替えですね。
詳しく説明していきます。
「同じものを含む順列」（重複順列）の考え方を使いますので、こちらの記事もあわせて読んでいただくと分かりやすいと思います。
関連記事：aaabbcの並び替え・重複順列・同じものを含む順列の解き方・計算方法～割る意味が目で見て一発で分かるように

 

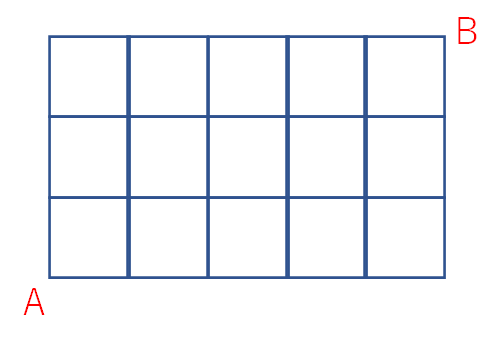
上の図で、AからBまで最短距離で行くのに何通りありますか、という問題です。
答えは既に①で求めています。56通りです。
今回はこれを計算で求めていきます。

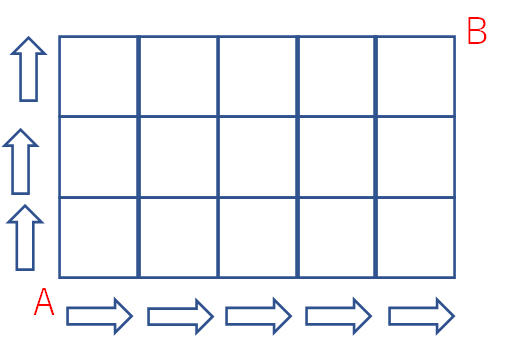
上の図を見てください。AからBまで行くためには、右に5回、上に3回移動する必要がありますよね。
この右と上の移動の順番はバラバラに組み替えることが可能です。とにかく合計で右に5回、上に3回移動していれば良いわけです。

例えば、→↑↑→→→↑→と移動したとしましょう。計→が5回、↑が3回です。
この場合は下の図のような移動になります。

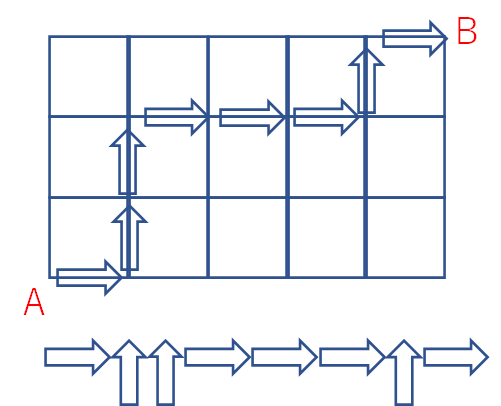
ここからが本題です。
AからBまで行く行き方をどうしようかな？　と考えるということは、つまり次のように言い換えられます。
「↑,↑,↑,→,→,→,→,→の8枚のカードを1列に並べる並べ方は何通りありますか」
という問題と同じことになるのです。
この問題ならば計算できますね。

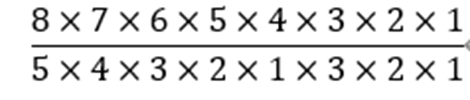
となります。答えは56通りです。（重複順列の考え方については今後別の記事で説明します）
このように並べ替えの問題に帰着させることにより、道順の問題を計算で解くことができました。

⑥立体の道順

⑤の平面の道順まででしたら、書き込む解き方でも、さほど問題はありません。
しかし立体の道順を解く際には、⑤で解説した計算で求める解き方がほぼ必須となります。
なぜかというと、数字を書き込んでいく方法では図がごちゃごちゃしてしまいミスの素だからです。
時間もたくさんかかってしまうので、是非計算で求める方法を使ってみましょう。

 

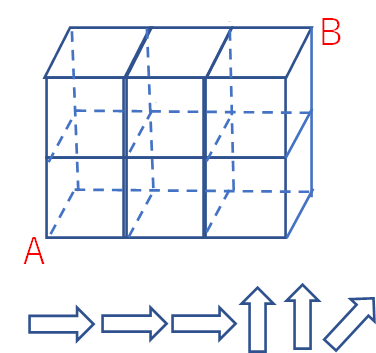
上の図のように、AからBまで最短距離で行く行き方が何通りあるでしょうか？　という問題です。
⑤で解説した計算で求める考え方を利用してみましょう。
AからBまでには、右→に3回、上↑に2回、奥↗1回移動すれば良いですね。

ここから同じものを含む順列的に考えると
「→→→↑↑↗を1列に並べます。並べ方は何通りありますか？」
という問題になります。もっと一般化すると
「aaabbcの6つを1列に並べる並べ方は何通りありますか？」
と同じ問題だということになります。
よって式は下のようになります。

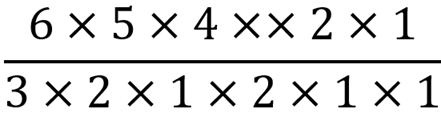
以上6パターンの道順問題を解説してみました。
ブログ記事ですのであまり深入りはせず、概要の説明に留めました。
この6パターンの道順が理解できれば、中学受験での応用問題にも十分太刀打ちできるようになります。

テストや入試で道順の問題が出た際には、どのパターンの道順なのかしっかりと考えて解くようにしましょう。

場合の数に関する別記事はこちら
リンク：場合の数の解き方の本質は全部同じ。樹形図を簡単にしているだけ！

下のにほんブログ村のリンクから、色々な先生の中学受験の指導法ブログを確認できます。（算田数太郎もランキングに参加しています。）
にほんブログ村

質問・相談・お仕事の依頼はこちらのメールアドレスへどうぞ
sandasuutarou3.14@gmail.com
（2020年度の家庭教師としての指導は難しいかもしれませんが、空きが出たらご案内します。ご相談ください。）