回転体の体積や表面積を求める問題でお困の方は必見の記事です。
回転体の問題とは次のようなものです。
問題:下の図の図形を直線Lを軸として回転させたときにできる図形の体積を求めなさい。
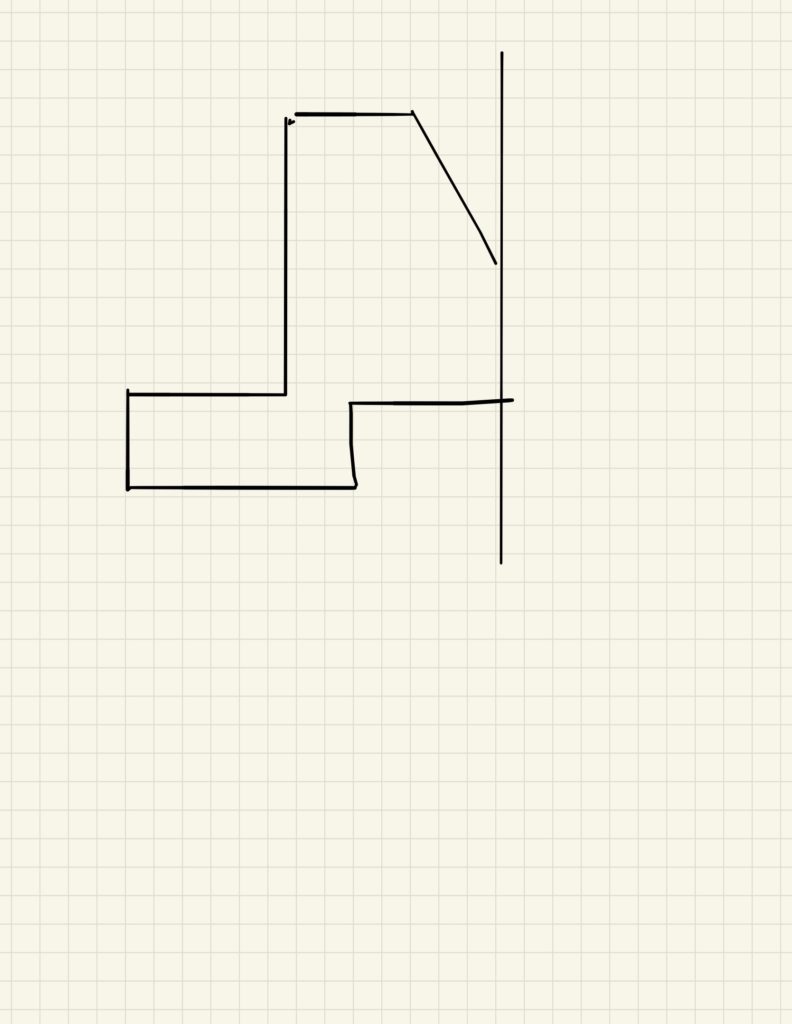
このような問題です。(例題なので数値は書き入れていません)
ipadでかいているため図が上手ではないのは見逃してください!
この問題の何が難しいかというと、回転させた際にどのような立体になるのか想像しづらいという点です。
回転された後の図が示されていれば解けたとしても、そもそもどんな形になるのか分かっていなければ計算のやりようもありません。
この問題を初めて見た子供がまず考える自然な行動としては、下のような感じではないでしょうか。一般的な小学6年生男子の問題用紙を再現しております。
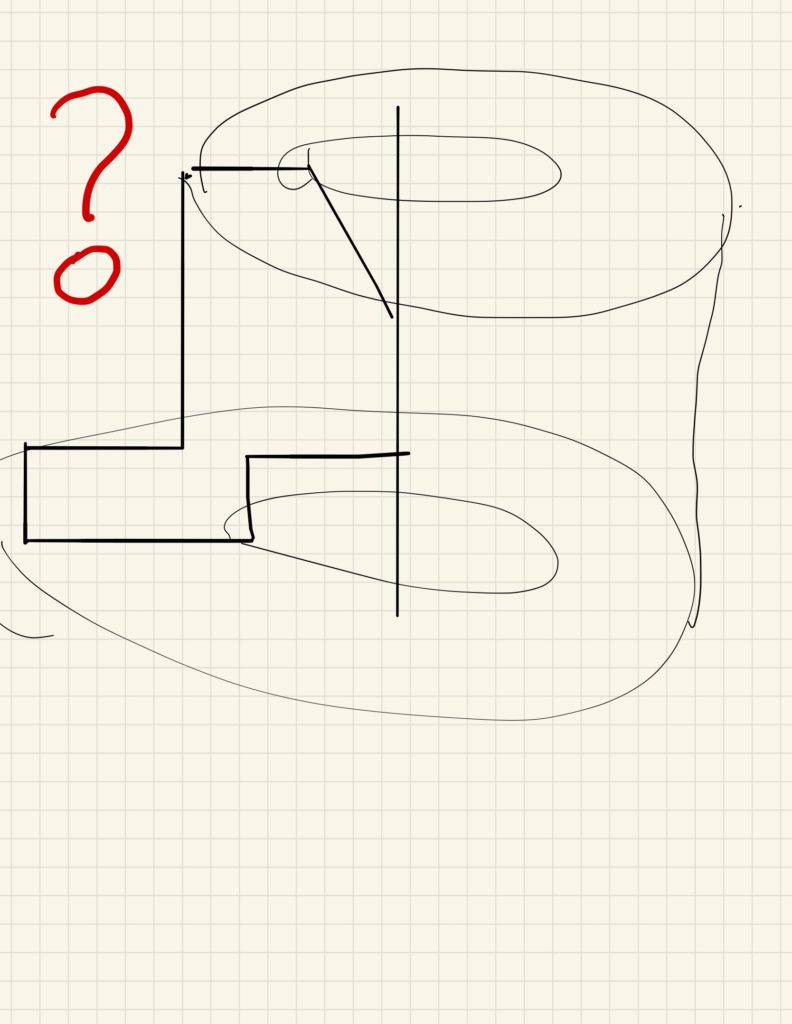
回転した後の形を作図によってなんとか把握しようと頑張るのではないでしょうか?
指導をしていると、このような図が残された問題用紙をよく目にします。
この方法で解くのには無理があります
なぜかと言えば、複数の問題点を同時に処理しようとしているからです。
複雑な問題は切り分けて一つずつ処理していきましょう。
問題の細分化です。
太古の昔から大軍を打ち破る方法は一つ。分割して各個撃破です。
順を追って説明していきます。
タイトルにもあるように、回転でできる立体は次の二つしかありません。
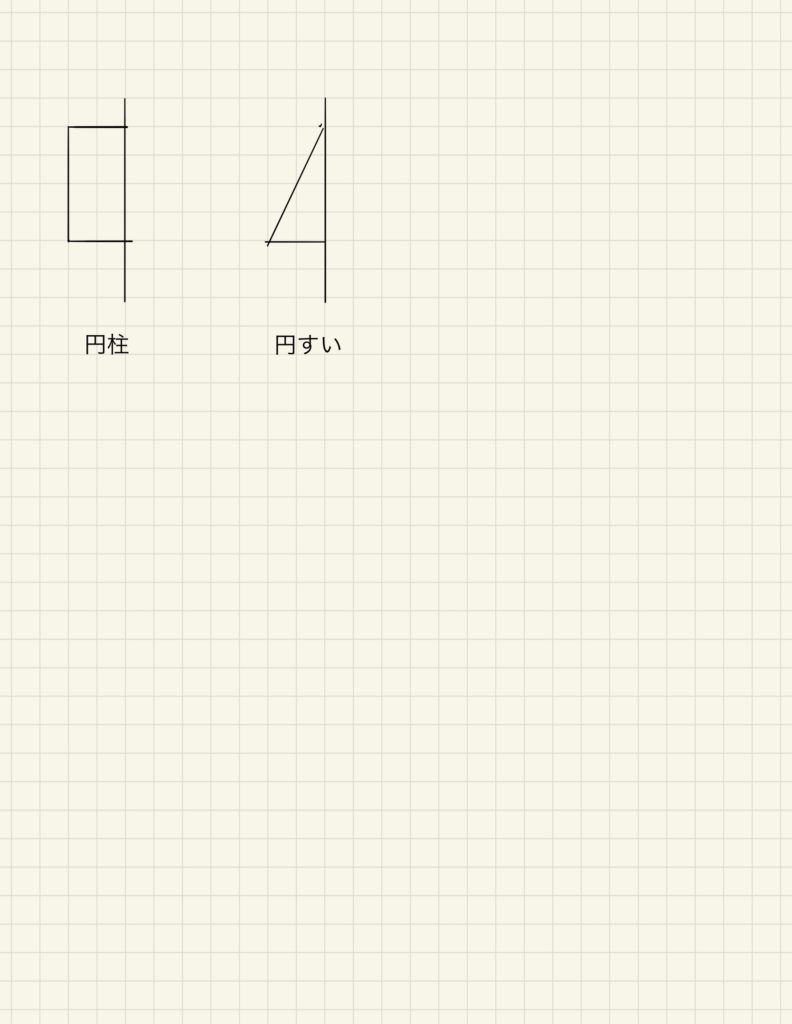
円柱と円すいの二つだけです。

そんな声が聞こえてきそうです。
下の図を見てください。
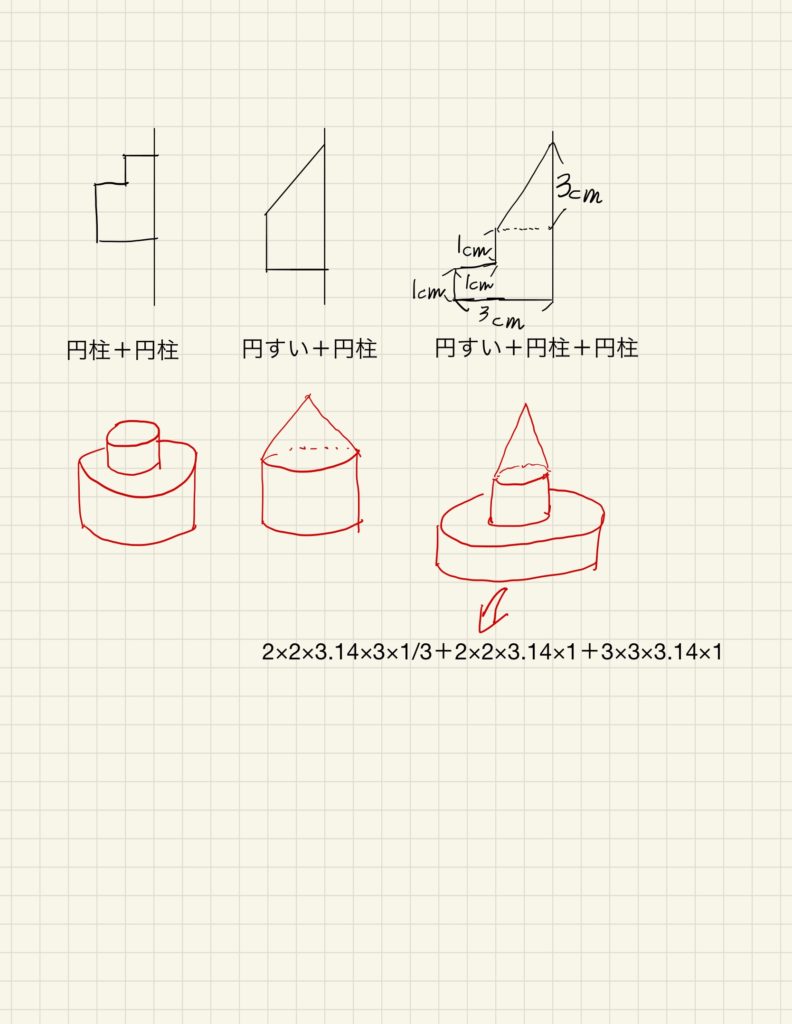
つまり一見複雑に見える立体でも、全ては円柱と円すいの組み合わせで構成されています。
すると右端の図形も、上の円すいと、真ん中の円柱と、下の円柱の体積をそれぞれ求めて足し算すれば答えが出せます。
もう少し複雑な図形に行ってみましょう。
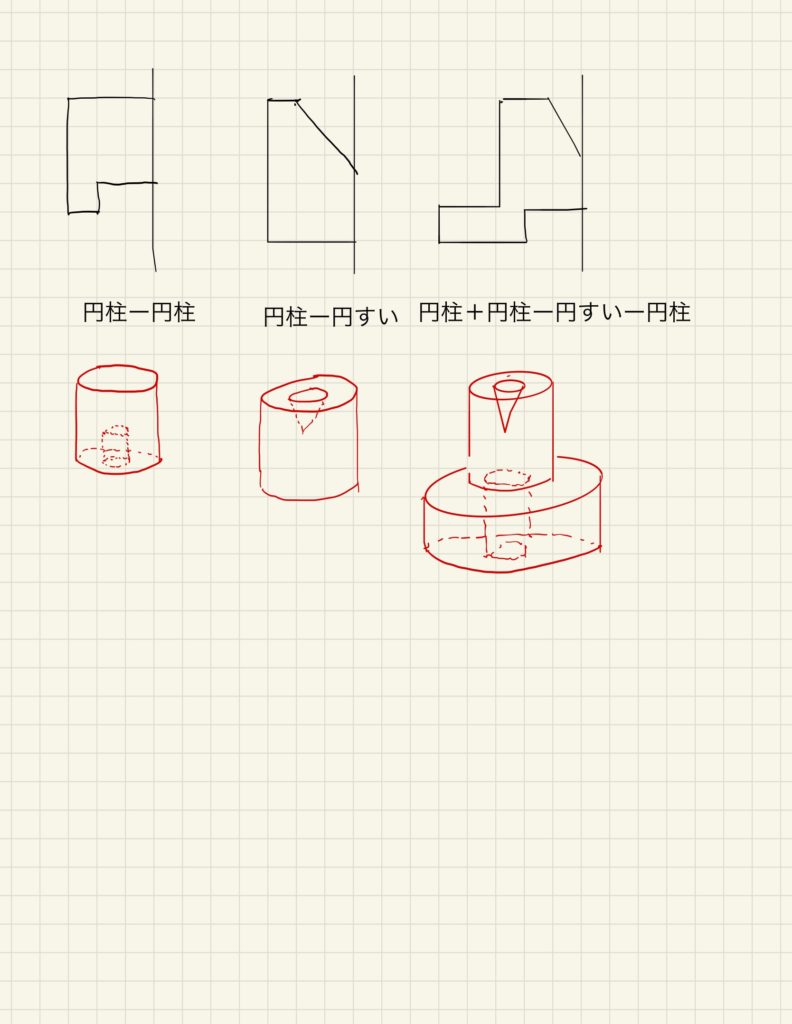
図形が少し複雑になりました。今度は引き算が登場する図形たちです。
左の図は、大きな円柱から小さな円柱を引いています。
真ん中の図形は、円柱の上部から円すいをくりぬいています。アリジゴクのような形ですね。
そして右の図形。この回転体の体積が問題で出たとしたら、どうしますか?
今なら考えることができるはずです。
まず基本となる形は、円柱の上に円柱が乗っている形です。
この上から円すいをひとつくりぬきます。
さらに、下から円すいを引いています。
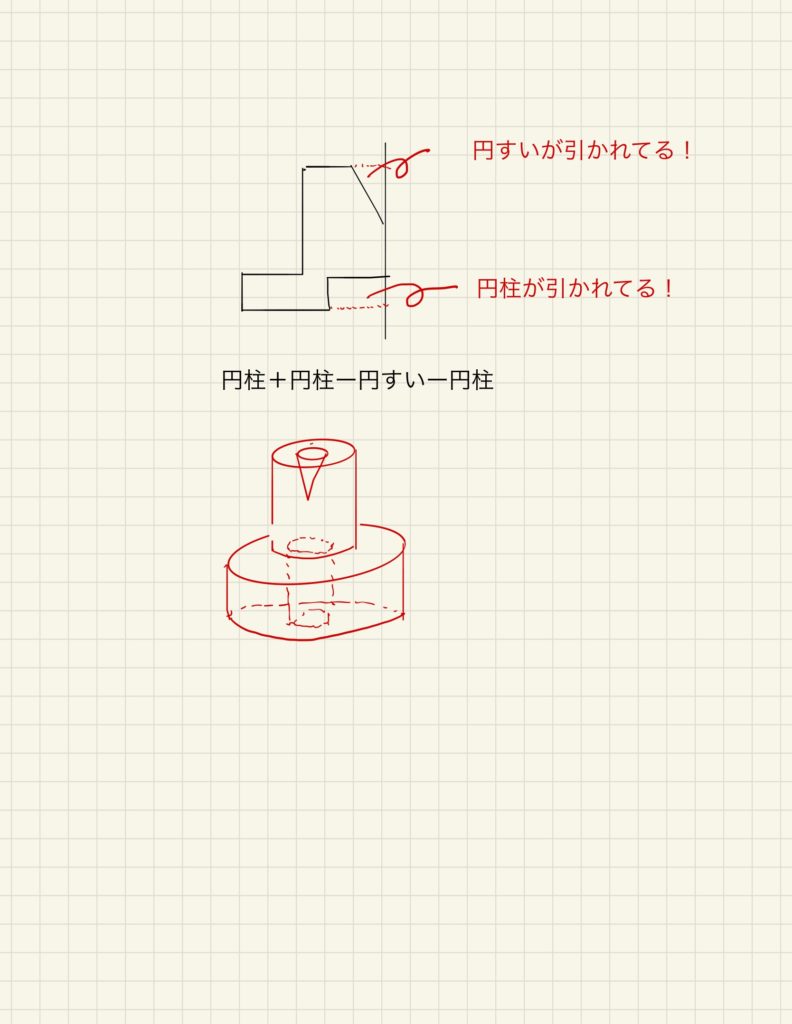
上の図を見てください。
問題文の図を見た際に「ここは円すいが引かれているんだな」「こっちは円柱が引かれているんだな」と、図形を細分化してとらえられています。
指導では生徒にこの状態になってもらうことを目指します。
問題の全体をぼんやりと眺めるのではなく、部分に分割して問題を捉えられるようになると、自力で解けるようになります。
そのための視点を提供することが、算数の導入指導で大切なことです。
ここまでのコツをつかんでしまえば、回転体の体積・表面積の図形を想像することは難しくなくなります。
このような方法で指導してあげれば、初めて見た問題でも自分で考えて解く力を付けられます。
「問題を分割するための視点」を教えてあげることが最重要です。
(もちろん子供向けにはもっとやさしくて面白い言葉で説明します。)
ご家庭で教えてあげる際にも参考になると思います。
是非真似してみてください。
