旅人算の問題は、6年生になるとほぼ全てが比を使って解く必要がある問題になります。
塾の先生の解説などでよく使われるワードに「比を使って解く」というものがあります。
このような抽象的な説明では、苦手な子はなかなかできるようにはなりません。
算数の先生をやっている人は算数が得意な人であり、どうしても得意な人目線からの説明になってしまいます。
「比を使って解く」とは具体的に何をしているのか?
もっと言うと「何を探せばいいのか?」というところまで具体化して考えていきたいと思います。
比を使うとはつまり何なのか・手順1問題文にそのまま書かれている比を見つける
まず最初に結論の一部を書いておきます。
速さと比の手順
手順1 問題文にそのまま書かれている比を見つける
手順2 ??????????
手順3 比の変換をする
手順2は最重要ポイントなので、最後に説明します。
それでは順を追って見ていきましょう。
旅人算の問題で登場する比とは、3種類あります。「速さの比」「時間の比」「距離の比」です。
この3つの比のうち、どれか一つが問題文の中に、ほぼそのまま書かれています。
(応用問題になると、これが分かりにくく書かれるようになります。発見が難しい比の見つけ方はまた別で解説します)
例えば、旅人算の問題でよくある書き出しに次のようなものがあります。
問題:太郎くんは分速50m、次郎くんは分速30mで同時に家を出発し、学校に向かいました。太郎君が学校についてから10分後に次郎君が到着しました。家から学校までは何㎞ですか?
こんな問題があったとします。
この問題において、手順1の 「問題文にそのまま書かれている比」は、速さの比です。太郎と次郎の速さの比が5:3です。これが第一歩です。
この手順1は、あまりにも当たり前すぎて逆に見逃してしまう子が多いです。
なぜ見逃してしまうのかといえば、これが最重要情報であるという意識を持てていないからです。
そのため、「手順1」と明確に区切って重要さをアピールすることにしています。
子供に伝えるときは「ここが大事だ」と言うだけでは伝わりません。重要だと認識しやすい形式を作ってあげることが必要です。
さて、手順1で速さの比が分かりましたね。次に本当は手順2が入るのですが、先に手順3の「比の変換をする」とはどういうことなのかを説明していきます。
例えばこんな問題です。
例題1:AさんとBさんの速さの比は3:2でした。二人が同じ時間歩いた時、2人の進んだ距離の比は何:何ですか? 答え:3:2
こんな感じです。速さの比が3:2の二人が同じ時間歩いたのなら、進んだ距離の比はそのまま3:2になりますよね。
ここでは 速さの比→距離の比 の変換が行われています。問題文では速さの比が与えられていて、それを時間の比に置き換えることで答えを出しています。
すると例えば次のような問題
例題2:AさんとBさんの速さの比は3:2です。二人が同時に出発して同じ時間だけまっすぐな道を同じ方向に歩いたところ、二人の間の距離が200mになりました。Aさんは何m歩きましたか。
これも例題1と同じように解いていきます。二人の速さの比が3:2なので、同じ時間歩いたのなら進む距離の比は③:②です。二人の間の距離が200mなので、③と②の差の①が200mになります。
ですから、Aさんが歩いた距離は200×3=600m と求められます。
速さの比→距離の比の変換以外にも
例題3:AさんとBさんの速さの比は3:2です。二人が学校から図書館までの道のりを歩きました。かかった時間の比は何:何ですか? 答え2:3
このように、速さの比→時間の比 の変換パターンもあります。 もちろん時間の比→距離の比、時間の比→速さの比、距離の比→速さの比、距離の比→時間の比 も併せて全6パターン、すべて存在します。
読み飛ばしても構わない脱線話
よくある中学受験の指導法として「速さの比と時間の比は逆比!」と呪文のように覚えさせる先生がいますが、これは長期的にみると非効率な教え方だと思っています。
算田は「逆比」という言葉は指導の際にはあまり使っていません。
比が逆になるという現象は名前を付けて覚えるものではなく、体感として理解してほしいからです。
その現象に名前を付けて識別するかどうかは、指導の際に結構大事なところです。
解法をパターンに分けて、そのパターンを一つのまとまりとして認識してほしい時には、子供向けに特徴的な名前を付けます。
ネーミングは大事です。
速さの比、時間の比、距離の比はそれぞれどの比にも置き換わることがあります。
ですから
手順1 問題文にそのまま書かれている比を見つける → 手順3 他の比に変換する
という手順になります。
あれ?飛ばした手順2は何だったの???
お待たせしました。それでは満を持して手順2の発表です。
手順2 一定のものを見つける
です!
速さの比 → 時間の比 におきかえるためには、距離が同じでなければなりません。つまり
問題:AとBの速さの比は3:2です。二人が同じ距離を進みました。かかる時間の比は? 答え:2:3
は問題として成立しますが、次の問題は問題として成立しません。
問題:AさんとBさんの歩く速さの比は3:2です。Aさんは家から学校まで歩き、Bさんは東京駅から青森駅まで歩きました。かかった時間の比は? 答え:わからない
極端な例ですが、距離が一定でなければ 速さの比→距離の比 の変換はできませんよね。(※比の合成についてはここでは触れません。)
ですから手順としては
ポイント
手順1 問題文にそのまま書かれている比を見つける
手順2 手順1で使った比以外の2つの比の中から、一定のものを見つける
手順3 残った1つの比に変換する
この手順になります。注目すべきは、「問題文に書いてある比をどの比に置き換えようかな?」という思考ではなく「一定のものはないかな?」と考えるということです。
何の比に置き換えることになるのかは、結果論でしかないのです。
実際に問題を解く際に考えることは、何の比に置き換えるかではなく、一定のものはどこかにないかと探しています。
これが、旅人算の得意な子が無意識にやっていることです。
最後にそこそこの難問を例にして、比の変換の考え方を実際にどう使っていくかを紹介して締めたいと思います。
問題
A,B,Cの3人が、ある地点から同じ方向にそれぞれ一定の速さで出発しました。最初にAが出発し、4分後にBが、さらに2分後にCが出発しました。そして、Bは出発してから8分後に、Cは出発してから10分後に、それぞれAに追いつきました。CがBに追いつくのは、Cが出発してから何分後ですか。
ラ・サール中学の問題です。
読者である保護者の方々は問題文の細部まで読まなくても大丈夫です!
下に線分図を載せておきます。
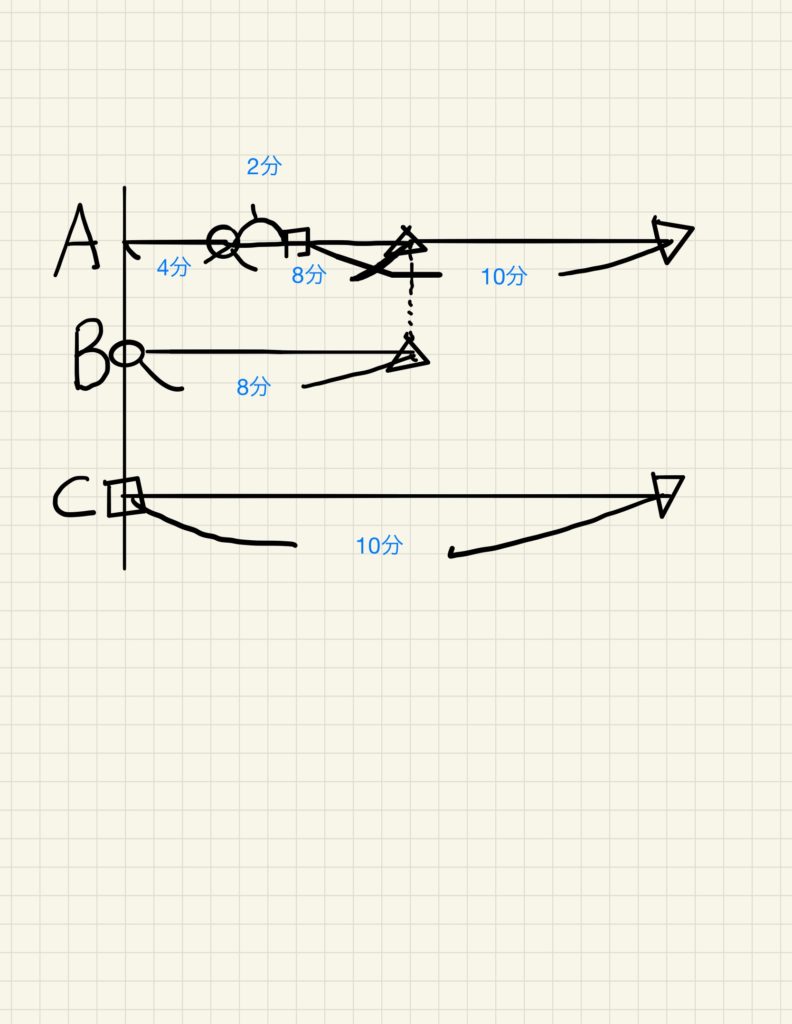
このような線分図は練習
すればだれでも書けるようになります。もし作図が苦手だという人は、ここだけは練習してかけるようになっておきましょう。
さて、上で説明した手順によれば、手順1は「問題文にそのまま書かれている比を見つける」です。
文中には時間の条件しか書かれていませんので、まず最初に分かる比は時間の比になります。
次に手順2の「一定ののもを見つける」に移ります。距離か速さのどちらかで、一定のものを見つけます。
今回の問題では、AとBとCの速さは異なりますので、速さが一定を利用する可能性は低そうです。
距離が一定の場所があるのではないかと予想します。つまり、二人の人が同じ距離を進んでいる区間はないだろうかと予想を立てて探していきます。
すると、下の図のように見つかります。
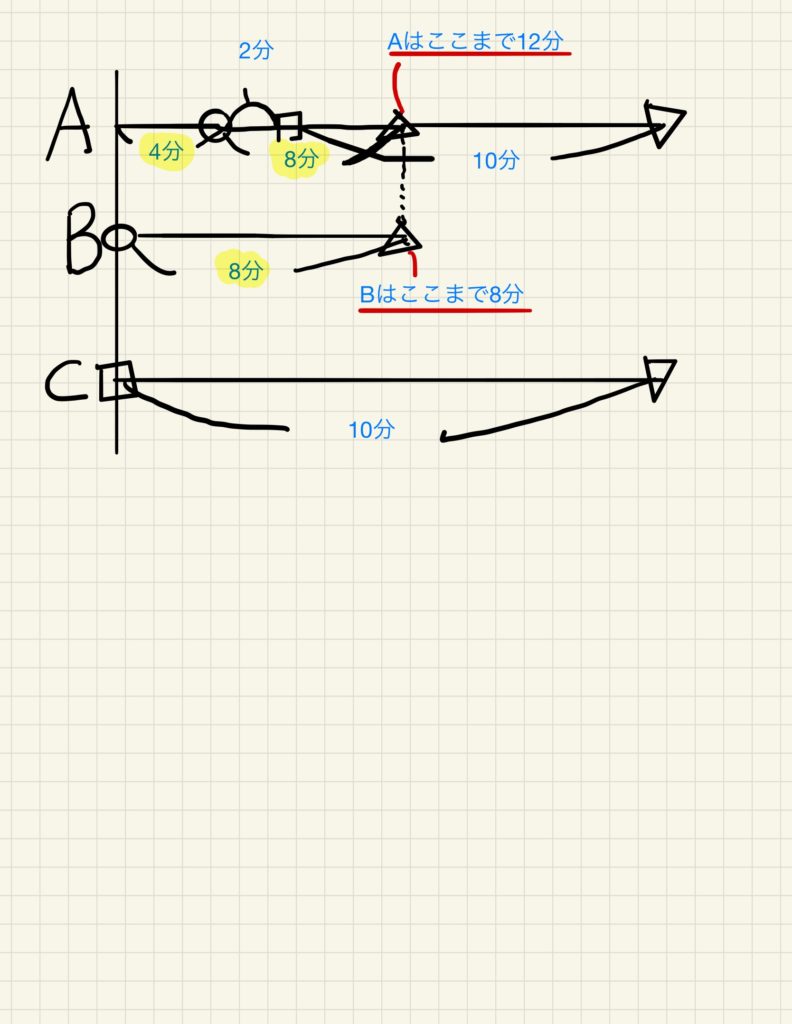
出発してから△のところまで、AとBが同じ距離を進んでいます。
同じ距離を進むのにかかった時間が、Aは12分でBは8分です。
同じ距離を進むのにかかった時間の比が12:8、つまり3:2ですので、AとBの速さの比は2:3となります。
後は同様に、AとCの速さの比を出して、計算していきます。この先は省略します。
これはほんの一例ですが、「比を使って解く」を具体的な手順に分解するとこのようになり、この考え方に従って進めていくと、結構な難問も誰でも解けるようになります。
……というと大げさでしょうか。
でも、使いこなせるようになるまでしっかり指導すれば元の偏差値にかかわらず、速さと比の問題だけは高レベルで解けるようになります。
昨年に入試が私は指導していた生徒で、6年生の途中から指導し始めた子がいました。算数の偏差値がサピックスで30台~40前半だったのですが、旅人算の線分図の描き方と、速さと比の考え方を徹底的に教えた結果、この種の問題はかなりのレベルで解けるようになりました。
魔法のような図や特殊な解法を使うわけではないので、一見しただけでは魅力が伝わりにくいのが難点ですが。笑
その分汎用性が高く、かつ本質の理解に役立つので、かなり有効な指導法だと考えています。
なるべくセンスに頼らない解法を。
センスのある人が無意識にやっていることを、センスがなくても意識すれば使えるように。
これが指導のモットーです。
記事はここまでです。良かったら他の記事も読んでいってください。
