N進法という単元があります。2進法や3進法などです。
例えば2進法とは「0,1」の2つの数字だけで数を表す方法で、2進法で「1110」と書くと10進法(普段私たちが使っている数字)では14を表します。
N進法に関する問題の難しさは大きく分けて2つあります。
①その問題がN進法であることに気づく
②気づいた後でN進法の計算をする
この二段階の難しさがあります。
大人から見ると②の難しさが目につきますが、実はそもそもその問題がN進法だと気づけないケースもあります。
例えば次のような問題を見てみましょう。
問題:白いカードが4枚と銅色のカード1枚が交換できます。銅色のカード4枚と銀色のカード1枚が交換できます。銀色のカード4枚と金色のカード1枚が交換できます。
今ここに金色のカードが2枚、銀色のカードが3枚、銅色のカードが1枚、白いカードが3枚あります。このカードを全て白いカードに交換すると何枚になりますか?
この問題はまさに4進法の問題です。
しかし一見してそのことに気づくためには、何度か類題を解いて慣れておく必要があります。
N進法であることに気づけないと、解法を覚えていたとしても解くことができません。
N進法の勉強ではまず第一段階として「その問題がN進法だと分かった状態で解ける」を目指します。
次に「一見N進法だと分かり辛い問題がN進法であることを見抜く」練習をするという二段階になります。
そのため第一段階の「その問題がN進法だと分かった状態で解ける」ところまでは省エネで勉強してすぐにできるようになりたいのです。
本番は第二段階ですから。
第一段階の勉強はサッとクリアし、第二段階の勉強をする時間を多く取りたいです。
今回の記事ではこの第一段階である、N進法だと分かった状態なら簡単に解ける方法を解説します。
これをクリアして、第二段階の勉強に進めるようになりましょう。
実際に生徒に指導する際には「そもそもN進法とは何なのか」や「我々が普段使っている位取り数記法」、「人類が10進法を採用しているのはなぜなのか」と言った根本のところから話して説明しますが、今回はそれは割愛します。
シンプルな解き方
私は「N進法ボックス」と呼んで生徒に教えています。
シンプルな解き方ですので、簡単に覚えられると思います。
先ほどの例の、2進法の「1101」を10進法に置き換えることを考えます。
下の画像をご覧ください。
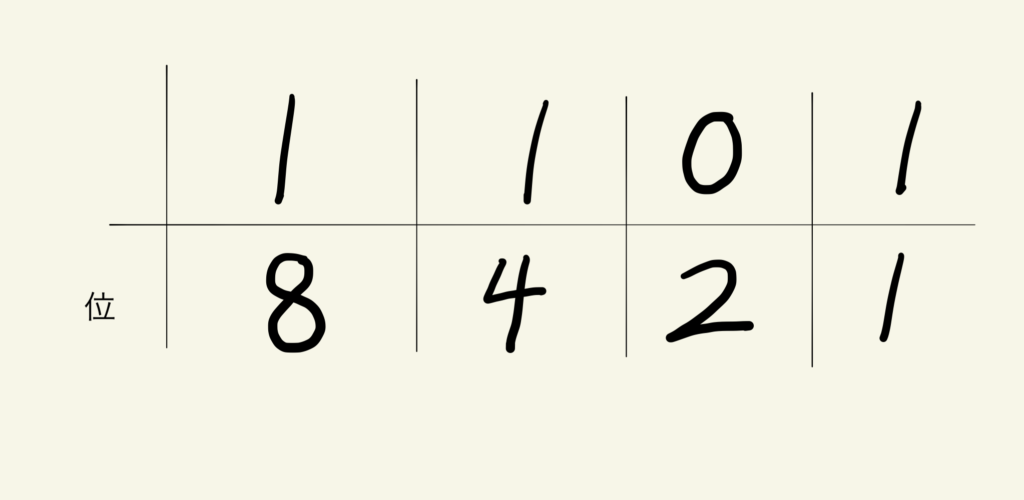
上下に分け、まず下段には「位(くらい)」を書き込みます。2進法の場合であれば、右から順に1の位、2の位、4の位、8の位です。これを2進法ボックスと呼びましょう。
2進法ボックスが出来たら、その上に2進法の数字を書き込むだけです。「1101」ですので、上の図のように書き入れます。
8が1個、4が1個、2が0個、1が1個という意味です。8×1+4×1+2×0+1×1=14 と求められます。
この問題はN進法→10進法の換算でした。 この逆もやってみましょう。
問題:10進法の78を3進法で表しなさい。
※3進法とは「0,1,2」の3種類の数字のみで数を表す方法のことです。
この場合も同様にN進法ボックスで解いていきます。
まずは3進法ボックスを作りましょう。
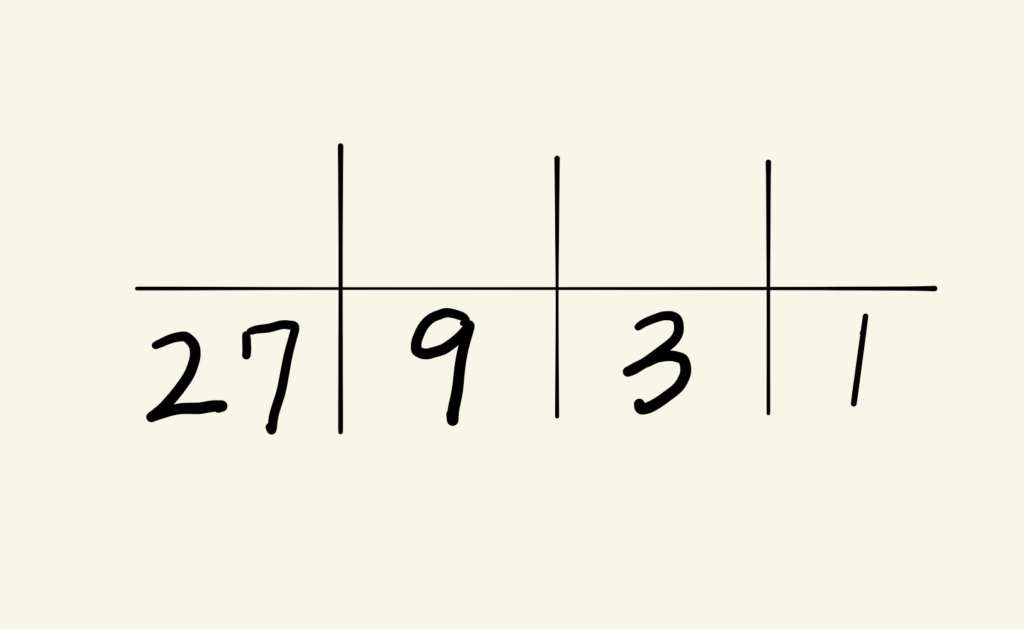
3進法の場合は、ボックス内の数字は左から順に(27,9,3,1)です。1から順に3倍ずつ大きくなります。
ボックスの中に数字を入れていきましょう。「78」の中に27は2つ入ります。(78÷27=2あまり24)
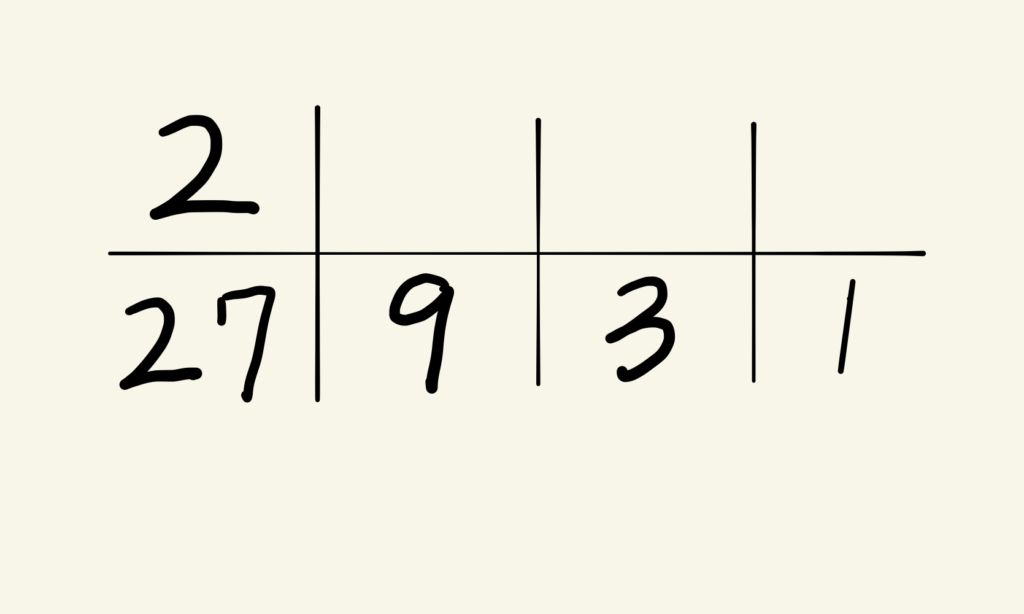
27の上に「2」を書き込みます。
次は先ほどの割り算のあまりである24を考えます。24の中に9は2つ入ります。(24÷9=2あまり6)
よって9の上のボックスには2を書き込みます。
次いで、あまりの6の中に3は2つ入ります。(6÷3=2あまりなし)
よって3の上のボックスに2と書き込み、割り切れているので次の1の上のボックスには0を書き込みます。
すると下の画像のようになります。
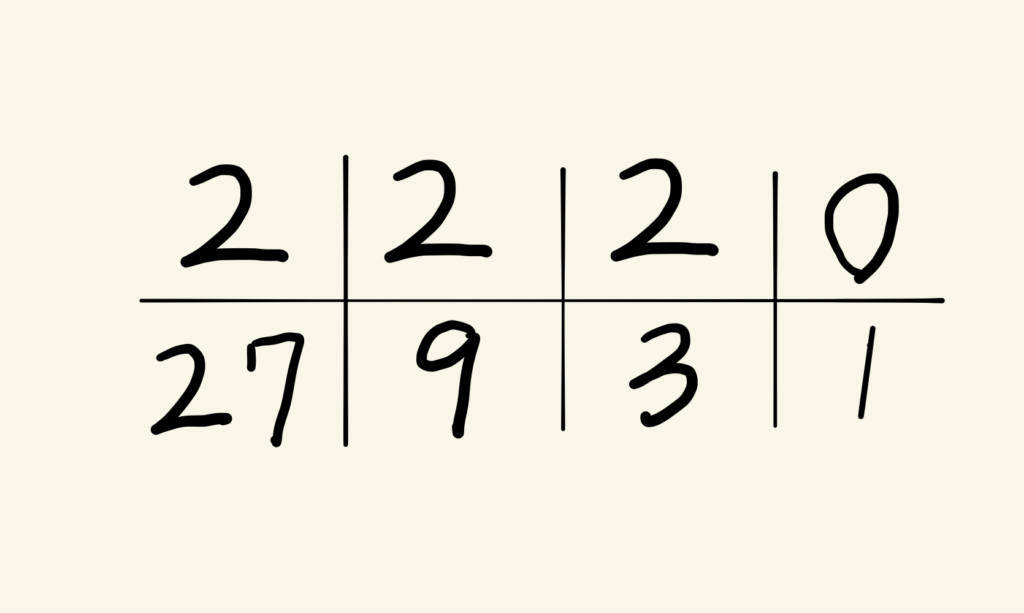
以上より、10進法の78を3進法に直すと「2220」であることが分かりました。
このボックスの書き方は、N進法の本質である「位取り」の表記法を分かりやすく表したものです。
実際の指導の際には、このボックスを使ったテクニカルな方法を教えると同時に、位取りの表記法の本質の考え方も説明します。
(少し余談を。10進法の位取り表記法は現代人はみんな無意識に使っていますが、位取りを利用して数を表す方法は数学史上の大発見として扱われるくらいのすごいことなのです!
例えば日本の漢数字には位取りはありませんよね。「10」は「十」、「100」は「百」という別の文字で表記します。この「じゅう」という数を「1」と「0」を並べて書くことで表すという方法は、実は歴史上の大発見なのです!)
N進法の解き方には、他には連除法のようなものもあります。
マスターすれば連除法の方が早く解けるのですが、解法を忘れやすく、自分が何を計算しているのか分からなくなりやすいです。
N進法は入試頻出という程ではありません。「たまに出る」くらいです。
N進法の本当の難しさは冒頭で説明したように「その問題がN進法で解けることに気づく力」の方です。
単純なN進法⇔10進法の換算計算のところは、なるべく省エネで、暗記事項を少なく乗り切りたいです。
できるだけシンプルに、本質に近く、分かりやすい方法を選択して受験を乗り切りましょう。(もちろん既に連除法でマスターしているお子様はそちらでOKです!)
良ければ参考にしてください!
