連比というものをご存じでしょうか?
たとえば
「AさんとBさんの持っている金額の比は2:3、BさんとCさんの持っている金額の比は4:3です。A,B,Cの3人の持っているお金の比は何:何:何でしょうか?
【答え】
A:B=2:3
B:C=4:3 なので
A:B:C=8:12:9 と求めるような一連の流れのことを「連比」と呼びます。
この連比がなかなか理解できずに困る小学生が多いです。
算数が得意な子にとってはなんてことない単元ですし、大人からすると「なんでこれが理解できないの?」と困り果ててしまいような単元です。
今回の記事では
連比の一般的な解き方にとどまらず
①なぜ連比を理解するのが難しいのか?
②理解するために必要な考え方・概念
③具体的な指導法
の三つに分けて解説していきます。
一般的な解き方
まずは一般的な解き方からご紹介します。
これは大人からすると分かりやすいのですが、算数が苦手な小学生からすると理解しにくいようです。
しかしほとんどの塾・参考書ではこのように解説されていますので、念のためご紹介します。


この解き方ではなぜ理解できないのか?
大人からすると「分かりやすい!」と思うかもしれませんが、なぜ小学生はこの解き方・解説では理解できないのでしょうか?
「最小公倍数の12で合わせる」が意味不明
解説の中で使われる表現「最小公倍数の12で合わせる」は、よく考えると意味不明です。
我々大人は、その先できれいに比を合わせられることを知っているのでスルー出来ますが、初めて聞く子供にとっては「12!?なんで突然!?」と混乱します。
比の数字と量を表す数字の区別がついていないから
「Bさんは3だったのに、なんで12に増えてるの!?」と思ってしまいます。
比を始めて学習する子供にとってこの反応は自然なものだと思います。
これは「③のお金を持ってたものが⑫に増えた」のではなく「2:3と表現したいたものを8:12と言い直しただけ」ということを理解する必要があるのですが、この部分をていねいに掘り下げることなく授業が進んでしまうことが多いようです。
そのせいで、算数が苦手な子にとってはとても理解が難しくなっています。
いきなり便利な方法を教えているから
99%の解説で用いられる「最小公倍数の12で合わせる」というのは、実は工夫した上での便利な解法です。
原始的な発想では異なる解法を用いるはずです。
それが以下の画像の考え方です。

こんな考え方を紹介する授業・参考書はほとんどありませんが、こちらの方が直観的に理解しやすいと思います。
つまり「Bは③のお金を持っていて、Cはその3/4倍なのだから……分数で表すしかないのかーいやだー」
というような感想が自然なはずです。
後の項目で詳しく説明しますのでここではこのくらいにとどめておきますが、この原始的な考え方から少しずつ子供の理解・思考を導いてあげることが、急がば回れで一番近道だったりします。
算数に限らず、いきなり最初から便利で高度な方法を教えても良いことはありません。
小学生向けの具体的な指導法
私が生徒への授業で実際に行っている指導方法を公開いたします。
大谷翔平とうのき先生の所持金の比は2:1です
比を表す数字と量を表す数字の区別をつけるために、想像しやすい題材を使って生徒の理解を醸成していきます。
授業ではこんな話をしています。
佐藤くん(生徒)と、お友達の太郎くんの所持金の比は5:4でした。きみの方が少し多くお金を持っているね。
そして、大谷翔平とうのき先生の所持金の比は2:1です。どうだーすごいだろ。大谷の半分だぞ!?
さて、今から私が言うことは合っているでしょうか?間違っているでしょうか?
「佐藤くんの持っているお金は5で、大谷翔平は2だよね。だからきみの方が沢山お金を持っている」
どう?これは正しいかな?
こんな話をします。
これは直感的に間違っていると分かりますよね。
ここから、まったく別の比を比べてはいけないということを学びます。
この話の跡で、数字を〇や△で囲って区別することを指導していきます。
野球大好き星人がいました
マルイチの考え方の感覚を身に着けてもらうためのトレーニング・小話を紹介します。
マルイチの考え方とは
③=1200円 ならば
①=400円 であるし、
1600円=④である。
というような考え方のことです。大人にとっては至極当たり前のことですが、初めて比を学ぶこの中にはここで躓いてしまう子も多いです。
大人にとっては当たり前なので授業の解説でもサラっと流されてしまい「分かるよね?」くらいの説明にとどめられていることも多いです。
なので、この感覚的な理解を養うためのトレーニング法・小話をご紹介します。
それが「野球大好き星人」です。
野球大好き星人
あるところに野球大好き星人がいました。この人は野球が大好きすぎるので、全てのことを野球で考えます。
お誕生日会に18人の人が参加していたとします。これを見た野球大好き星人は「おっ! 野球チーム2つ分の人が参加しているな!」と思います。(野球チームは1チーム9人です)
同様に、9kgのお米のことは「1野球チームキログラムのお米だ」、270円のお菓子を見ると「30野球チーム円だ」のように、なんでも野球チームで考えてしまいます。
問題1:45個のリンゴがあります。これは何野球チーム個と言えるでしょうか?
問題2:8野球チーム冊の本があります。何冊ありますか?
※女子生徒の場合は「アイドルグループNewJeans大好き星人」などで説明します。
謎のスポーツ「ウノッキー」
宇宙で大流行のスポーツ「ウノッキー」大好き星人がいました。
この人は全てのものを「ウノッキー」単位で考えます。
しかしウノッキー1チームの人数は謎です。
たとえばリンゴが入った箱を見ると「3ウノッキー個のリンゴがあるよ!」のように認識します。
さて問題です。
箱の中に5ウノッキー個のリンゴがありました。2ウノッキーのリンゴを食べました。残りは何個でしょうか?(地球の単位で答えられない場合は、宇宙語の単位を用いても構いません。)
→答えは3ウノッキーです。何個あるかは分かりませんが、未知の単位「ウノッキー」を使えば表現することができますね。
さて、「ウノッキー」と毎回書くのも疲れるので、今後は3ウノッキーのことを③を書くことにします。これでも分かりますよね。
では問題です。8ウノッキー円の貯金がありました。あ、間違えた。⑧円の貯金がありました。③円のおもちゃを買った所、残りは400円でした。
さて、①とは何円のことでしょうか? また、最初は何円持っていましたか?
※女子生徒の場合は「謎のアイドルグループ・オールドジーンズ」などで説明します。
大人向けの解説
一見するとふざけた解説のようですが、マルイチを理解するための大切な考え方が含まれています。
ここで目指しているのは、比の数である「3:4」のような数字を、マルで囲って「③と④」のようにすることで、実体のある数量として扱えるようにするということです。
ただ比を表すための数字ではなく、⑤とは実は400円のことなんだよ、というように、実体の数字を伴ったものであると捉えられるように子供の認識を操作することを目的としています。
大人からすると当たり前すぎて、なんでこんな簡単な所に手間と時間をかけているのかと不思議に思うかもしれないのですが、小学生が比を理解するためにはこんなストーリーとともに体験するのが分かりやすいのです。
原始的な方法から少しずつレベルを上げていく
Bさんの数字が同じパターン
例題:AさんとBさんの所持金の比は2:3です。BさんとCさんの所持金の比は3:5です。A:B:Cの所持金の比を求めなさい。
この問題であれば、理解できる子が多いと思います。
Bさんに相当する数字が同じなので、スムーズに連比に持ち込めます。
このような図を書いて、四角的に分かりやすくしてあげるといいでしょう。
(新しい図を導入する際は、簡単な問題を例にして説明すると良いです)

Bさんの数字が同じが簡単に割り切れるパターン
例題:AさんとBさんの所持金の比は5:6です。BさんとCさんの所持金の比は2:1です。A:B:Cの所持金の比を求めなさい。
この問題は、Bさんの数字である「6」が2で割り切れるので次のように直観的に理解しやすいです。
CさんはBの半分ということは……3だ!
こんな感じです。
もしここがスッキリ理解できないときは、前段の「野球大好き星人」と「謎のスポーツウノッキー」の理解が抜けているので、この二つのトレーニングから先にやるようにしてください。
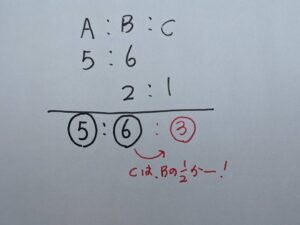
分数にしたくないよね!
例題:AさんとBさんの所持金の比は5:4です。BさんとCさんの所持金の比は3:1です。A:B:Cの所持金の比を求めなさい。
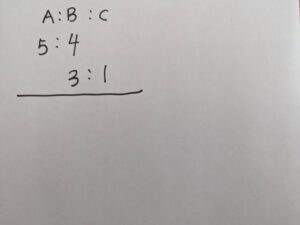
この問題が、最終的に理解したかった問題です。
多くの教科書には、以下のような説明が載っています。
「まずBさんの値を、3と4の最小公倍数である12で合わせます。そして~」
はい、この時点で小学生の約半数が脱落しています。
「最小公倍数で合わせる」というのは工夫の結果であり、いきなりこれを教えるのは違うと思っています。
まずはこんな風に考えてみるべきです。
A:Bが5:4か。⑤と④としておこう。さて、CさんはBさんの三分の一だから……ええ!?4÷3は分数になっちゃうじゃーん!!!
この「分数になってしまう嫌な気持ち」を大事にしたいです。実はここが出発点なのです。
次に、このように生徒に話しかけてみます。
「Bさんが④だから嫌なんだよね。これがもし⑥とか⑨とかだったら楽じゃない?」
そうなんです。Bさんの値が3の倍数だったら嬉しいんです。
そこで、次にこんな話をしてみます。
「さて、話は変わるんだけど、5:4と10:8って同じだよね。他に、5:4と同じものって書ける?かけるだけたくさん書いてみよう」
ということで、5:4、10:8、15:12、20:16……としばらく書いていきます。

「これは全部同じものだから、5:4と書くべきところを例えば25:20って書いても別にまぁ間違いじゃないよね。ふつうやらないけどさ。さて、さっきの問題で連比するときに『5:4』と書いたけれども、その部分は今列挙した比と入れ替えてもまぁ間違いではないわけだ。だからここを10:8と書いても間違いではない。さて……どれに書き換えたら、計算が楽になるかな?」
とこんな感じです。3で割り切れる数にしておくのが良いので、15:12が選ばれると思います。
あとは一般的な普通の解説と同じです。
「Bさんを12に置き換えるとラクになった」という経験を一度しておけば、そのあとはよくある解説の「最小公倍数の12で合わせる」の意味と目的が納得しやすいですし、理解がスムーズになります。


比の最初の導入の際には、このような感じで指導します。
つまり
①いきなり便利な方法を教えない
②最初は原始的な方法から学ぶ
③原始的な方法では困る!という経験をさせる
④工夫をする
こんな流れで学びます。
これをスモールステップの問題に区切って、手を動かして取り組みながら自然と学べるようにします。
小学生は、人の話を聞いて勉強するのは得意ではありません。
自分でやってみて、手と頭を動かしている時が一番学習効率が良くなります。
講師が教えすぎないように、でも正しい道筋に導いていけるように。
そんな感じで教えるとうまく行きやすいと思います。
苦手な子こそ、根本の理解を。暗記に逃げてはダメ
多くの指導者は逆に事をします。
算数が苦手な子は根本を理解するのは大変だから、まずは暗記で乗り切ろう。
これは逆効果だと考えています。
算数が苦手な子こそ、どれだけ時間をかけても最初に根本の理解をしておかないといけません。
得意な子であれば、最初は公式を暗記してもそのうち自分の中で理解できる日が来るかもしれません。
しかし苦手な子は、自分で公式の意味を考えたり、なぜその公式が成立するのかを解き明かせるだけの思考ツールがまだそろっていません。
なので誰かが最初にしっかり教えてあげないと、ずっと分からないままになってしまいます。
苦手な子であっても、正しい指導方法で時間をかけて教えれば、ちゃんと理解できるようになります。
出来る子と比べれば歩みはゆっくりですが、しかし着実に成長していきます。
そして成長できるということは、テストでの偏差値も徐々に上がっていきます。
長期的な教育の観点でも、短期的な受験合格の観点でも、どちらにしても根本の理解を目指した勉強方法の方が効果的です。
大手の塾のカリキュラムは早すぎる。時間が短すぎる
比の学習は中学受験カリキュラム全体を見渡しても最も大切な単元です。
そんな大切な比の単元が、2~3回くらいの授業で済まされています(例えば早稲アカの場合だと、夏期講習中に2回、9月の通常授業で1回)
算数が得意な子であればこの時間数でも十分かもしれませんが、苦手な子にとってはこの倍の時間数を書けても惜しくないくらいの単元です。
新しい概念の理解に必要な時間は上位生と下位生で大きく異なります。
しかし塾のカリキュラムは上位生に合わせて設計されているので、苦手な子にとっては苦しいです。
家庭教師の指導では、その子にとって最適で効果的な丁寧さで指導します。
5年生の比であれば、夏休みの間から予習を重ねておき、比を本格的に学習する9が月を余裕をもって迎えられるようにします。
お子様の中学受験の学習を、辛く苦しい暗記にしたくない方。
きちんと根本の理由を納得して、使える知識として成長していきたいと目指しているご家庭は、是非家庭教師のサポートをご検討ください。
2025年2月から指導開始のレギュラー生を現在募集しております。
ご興味ある方は、お問い合わせからご連絡ください。