平面図形と比の問題で、よく起きる混乱について解説します。
平面図形と比の問題には、いくつかの考え方の種類があります。
塾の解説ではこれらの種類の区別があいまいなまま、各問題ごとにバラバラに登場することが多いです。
場合によっては、同じ問題でも先生によって解説の方法が異なることもあります。
これでは「あれ、さっきに問題と急に解き方が変わったぞ!?」となってしまうでしょう。
どの考え方も本質は同じで、どの考え方を使っても問題は解けます。
しかし、問題によってはある考え方を使ってしまうと計算が煩雑になったりするので、使い分ける必要があります。
あれ、なんか急に考え方が変わったぞ? と混乱してしまうことを防ぐために
まずは3つの大きな考え方に分類します。
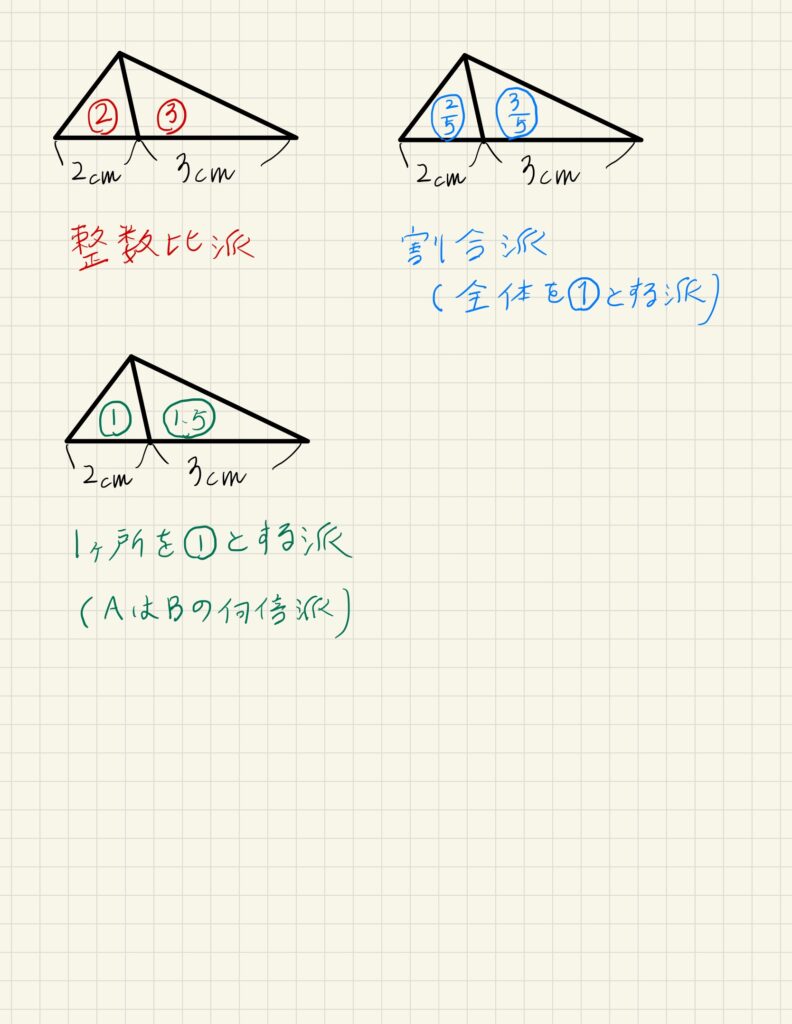
まず例として、高さが一定で、底辺の比が2:3である三角形について考えます。
この二つの三角形の面積を捉える際に、大きく分けて3つの考え方があります。
整数比派と割合派(全体を①とする派)と一か所を①とする派です。
この考え方を、少し応用させると次のような問題になります。
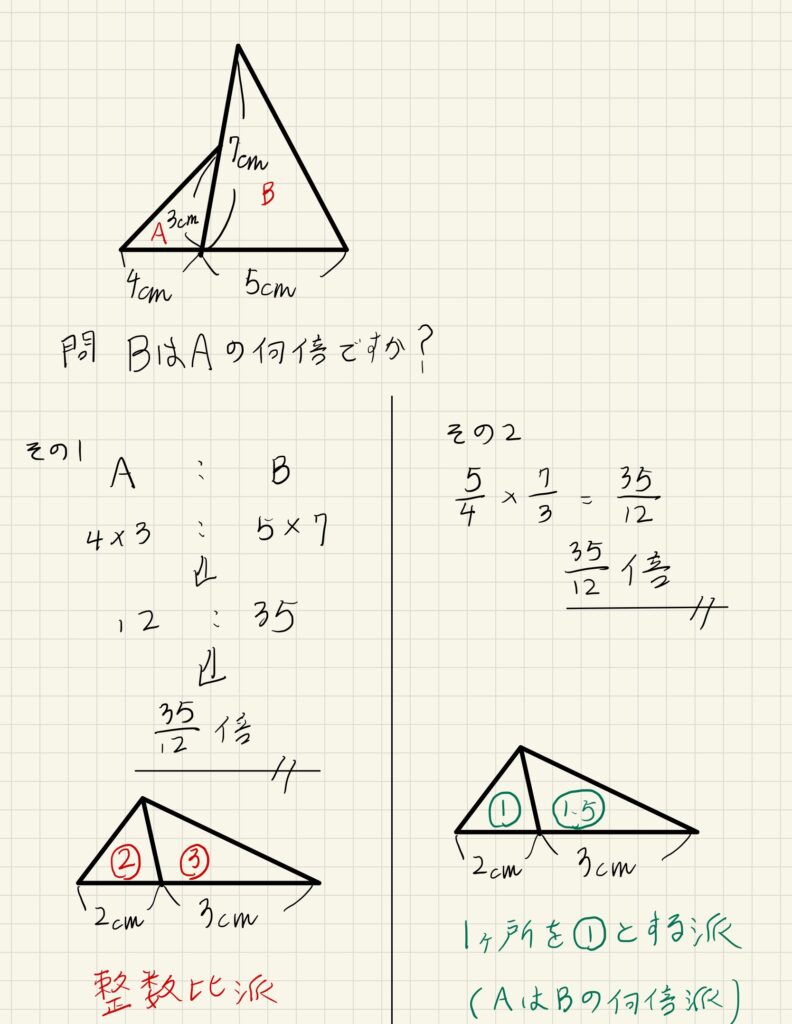
同じ問題であっても、整数比で考えるのが好きな人と、一か所を①として「〇倍」で考えるのが好きな人とでは式や解説の方法が異なります。
集団授業では、先生によって結構流派が分かれる印象があります。
上の問題でも、どちらの考え方の方が絶対的に正しいということはなく、どちらで解いてもOKです。
しかし気を付けなければならない点があります。
片方の考え方で解いた生徒が、塾の解説で異なる解法の解説を聞いた際に「あれ、この問題はこっちで解かなきゃいけないんだ」と思ってしまうことです。
実際にはどちらで解いても良いですし、どちらの考え方も理解して使えた方が良いです。
「良く分かんないけどなんか色んな解き方がある」ではなく「大きく分けて三つある」のように、考え方を類型化して教えることが有効です。
全体像が把握できて初めて「どれを使おうかな」と考えることが出来ます。どんな考え方があるのかが把握てきていなければ、その場で思いついて解法を無計画に使い、途中で違う考え方が混ざってしまい、混乱して間違えます。
(例えば、最初は一か所を①として解き始めたのに、途中から全体を①とした場合の数値と混ざってしまう。など)
平面図形と比の問題の根本の部分である、考え方の分類について解説しました。
※GW期間で算田の授業数が増えており、ブログを書く時間がとりづらくなっています💦 本当はもっと詳しく書きたいので……そのうち続きを書くかもです!
国語の複数人指導コースへのお問い合わせもいただいております。ありがとうございます。
4/30までにご連絡いただいた方は初回は無料ですので、ぜひこの機会にお問い合わせください。