和差算が分からない子にどう教える？簡単なことほど教えるのは難しい！

和差算というものをご存じでしょうか。
中学受験塾では4年生の一番最初の方で習う単元です。
問題としては次のような形式です。

さて読者の皆様でしたら、この問題が分からないという子にどのように教えるでしょうか？
大人からすると問題自体は簡単で、答えは12個です。解説の冊子にも
（20+4）÷2＝12　と書かれています。

問題はここから先です。この和差算が分からないという子の「分からない」をどこまで分解できるかが、算数講師としての力量の差なのではないかと思っています。
難問を綺麗に解説できる講師はそれなりの人数いますが、和差算がピンとこないという子に何を教えればいいのかを分かっている講師は非常に少ないです。
今回はチャレンジ企画として、算田数太郎なら和差算をこう教える！　を一部公開いたします。文字だけでどこまで皆様に伝えられるか、チャレンジです。

想定している生徒像としては、新小4から塾に通っている小学5年生の9月。4年生で習ったはずの和差算がいまいちピンとこず、問題も解けないというお子様です。

原因①数を線にするという感覚がない

「数を線の長さで表す」ということは、実はかなり高等な技術なのだと思っています。
大人は棒グラフ等で日常に馴染んでいますが、小学生にとっては未知の考え方です。

和差算は一般的には線分図を利用して考えます。
冒頭の問題であれば、次のような線分図を書きます。

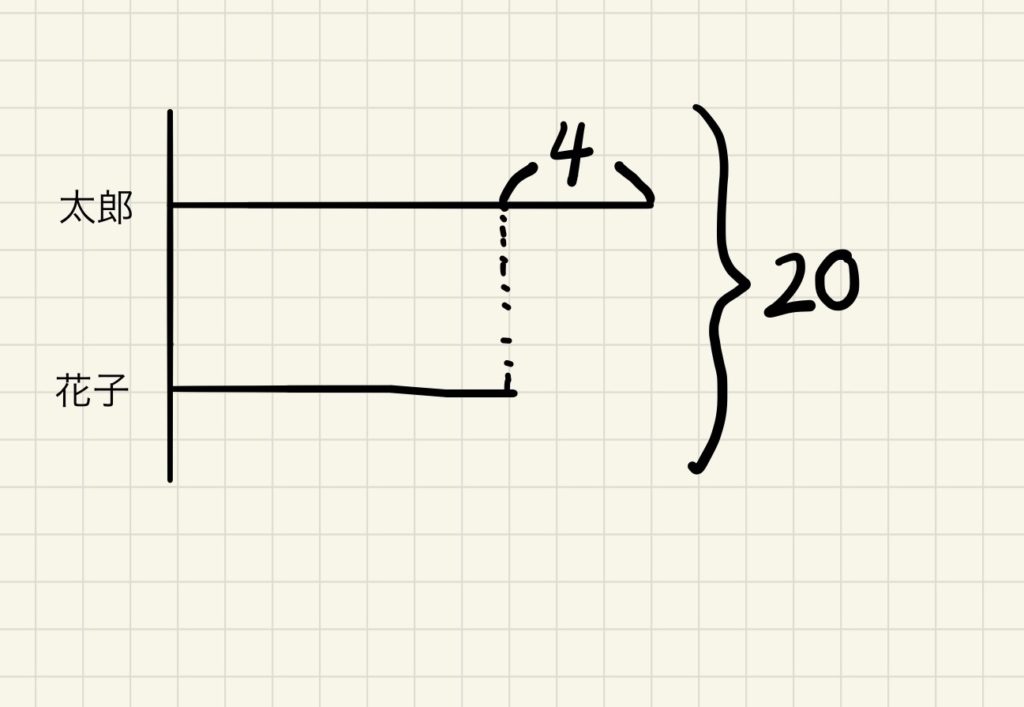
大人からするとこの線分図は当たり前のものに見えますが、算数が苦手な小学生にとって「数を線の長さで表す」ということは未知の領域です。
なぜ数が線の長さになるのか、この違和感から取り払ってあげる必要があります。

そのための練習問題は次のようなものです。

そして下の図を示します。

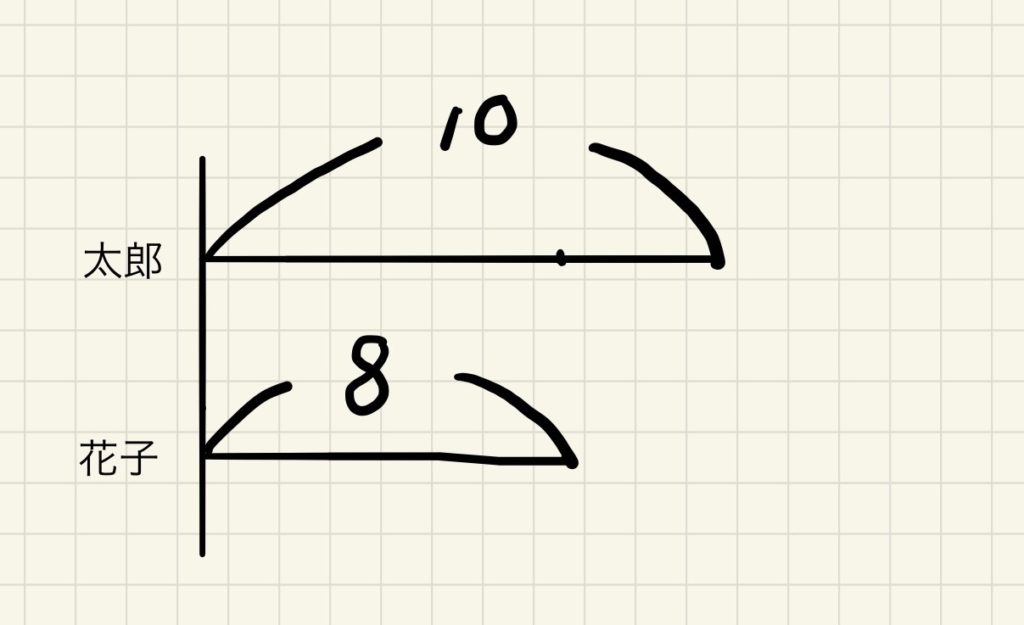
ただ二人の持っているリンゴの個数を線としてあらわしただけです。
この練習を挟むことでまずは「数字→線の長さ」をやっているのだという感覚が身に付きます。

次はこんな問題です。

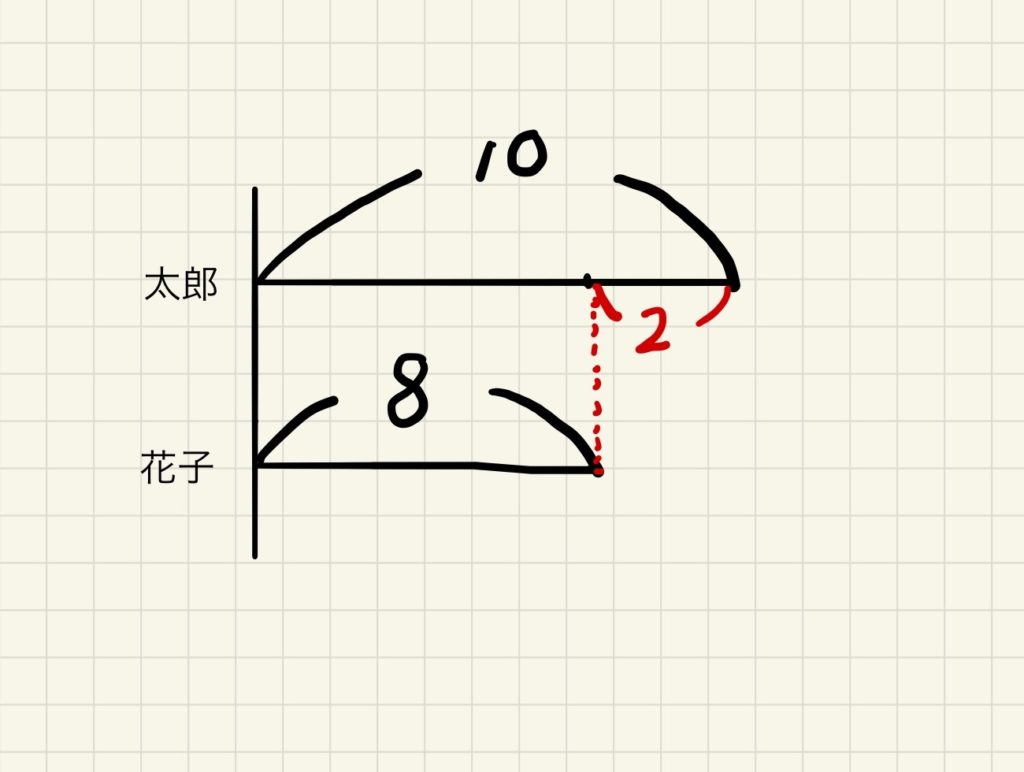
線の長さの差が、二人の持っている個数の差であることを意識付けます。

ここまで、「数の大小を線の長さで表す」という考え方の周辺を鍛えるトレーニングを紹介しました。
こうした「大人にとっては当たり前のこと」の説明が省略されて、いきなり応用から解説されてしまうので分からない子が発生します。

自分にとっては当然だと思っているけれども、生徒にとっては当然ではないことが含まれていないだろうか？と考えるようにしています。

個数が同じだったら簡単。という前提

突然ですが次のような問題はいかがでしょうか。

答えは当然8個です。線分図に書けば下のようになります。

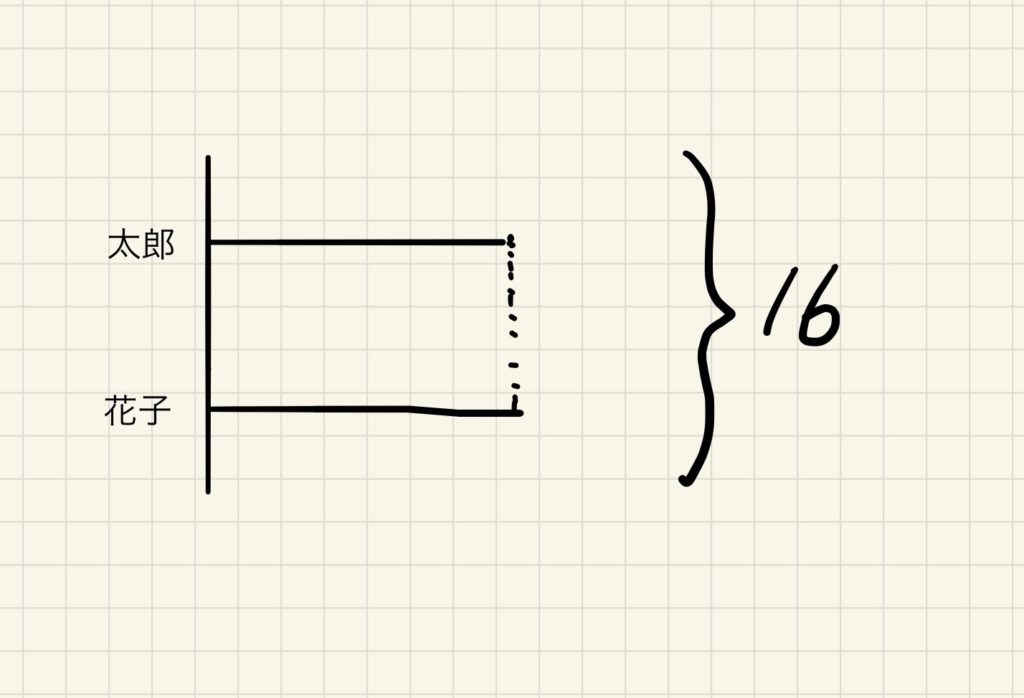
ここから分かることは「二人の個数が同じだったら、2で割るだけだから簡単」ということです。

なぜこの話をしたかというと、和差算の解法にはこのことが前提として含まれているのです。冒頭の問題

の解法は、まず20-4＝16とします。
その後で16÷2＝8として花子のリンゴの個数を出し
太郎はそれより4個多いので8+4＝12です。

この手順の冒頭「20-4」は何をしているのかというと、二人の個数が同じだったら÷2が使えるから、個数を揃えよう！　という発想です。
つまりゴールが先に見えている人の発想です。
分からない子はこの前提がないので、なぜ急に4を引いたのか理解できなくなります。
そのためには説明の順番を前後させて、「個数が同じだったら簡単に解ける」という前提をトレーニングを通して共有しておくことが必要です。

個数が同じだったら簡単だ→でもこの問題は個数が違う→同じだったことにして計算しよう

というように意識づけることで計算の意味を理解できるように促します。
大人にとっては当たり前に見えているゴールでも子供にとっては見えていません。
トレーニングを通じて意識付けし、計算の意味を理解できるようにすることが「本当の理解」だと思います。

まとめ

塾の先生や家庭教師は勉強のできる人が職に就くことが多いので「このくらいはみんな分かるだろう」の基準が高くなりすぎる傾向があります。

分からない子を分かるようにさせるということは、その子のレベルに合わせてカスタマイズした指導が必要です。
簡単な内容を子供に分かるように説明することは高いスキルが必要で、大人のとっての「前提」をどこまで排除できるかが腕の差です。
今回の記事では一番の初歩ということで和差算を例にしましたが、これ以外の単元も全て同様です。

文字だけではなかなか伝わりにくい部分もあるかと思いますが、少しでも伝わればと思います。
一般的な塾・家庭教師や、その延長線上程度の「プロ講師」を試して改善しなかったとあきらめる前に、是非一度ご相談ください。