今回は中学受験における場合の数、サイコロ問題を扱っていきます。
サイコロ問題にも「割るの?割らないの?」という疑問が付いて回りますので、その辺りを解消していきたいと思います。
突然ですが問題です。
問題1:大小2つのサイコロをふりました。目の出方は何通りですか。
問題2:赤青2つのサイコロをふりました。目の出方は何通りですか。
問題3:大きさも形も色も同じサイコロを2つ同時にふりました。目の出方は何通りですか?
いかがでしょうか。答えは、問題1と2が36通りで、問題3が21通りです。
今回のテーマは「サイコロにが大きさの違いがあるかないかで答えが変わる!」です。もっと言うと、区別するかしないかという点です。
まずは問題1と2です。この2問は全く同じ問題です。考え方としては
大きいサイコロの目の出方が6通り、小さいサイコロの目の出方が6通りありますので、
6×6=36 が答えになります。
※ここの計算方法が不安な方はこちらの記事をどうぞ:場合の数の解き方の本質は全部同じ。樹形図を簡単にしているだけ!
さて問題3に移ります。「え、問題3も36通りじゃないの?」という疑問があるかもしれませんが、違います。
問題3の2つのサイコロは、大きさも色も投げるタイミングも全て同じなので、区別がつかないのです。
問題1の場合であれば「大のサイコロが1、小のサイコロが2」と「大のサイコロが2、小のサイコロが1」は別のものとして数えますが、問題3では大きさき区別がないので、どちらも同じく「1と2」として数えることになります。
下の表で詳しく説明します。
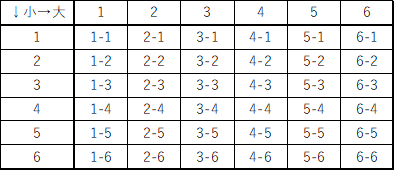
縦に小のサイコロの目、横に大のサイコロの目をとって表を書きました。
このように数えると、間違いなく36通りあることがわかります。
次に大小の区別がない場合を考えてみましょう。
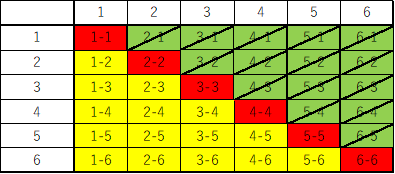
上の図で色分けしたところの、黄色と黄緑の部分は、同じものを数えています。
例えば「1-2」と「2-1」は同じものです。サイコロは全く同じものですから、見ている人からしたらどちらも
「あ、1と2の目が出たな」としか認識できないはずです。
そのため黄色と緑の部分は同じものなので、片方は数えません。
赤い部分は、ダブりがないのでそのまま数えてOKです。
したがって黄色と赤の部分を数えて、21が答えです。
※計算で求める場合は、例えば(36-6)÷2+6=21 のような式で計算します。
このように、サイコロに大小がある場合とない場合では答えが変わってしまうのです。
中学受験の場合の数の問題では、区別をつける設定での出題が多いので「大小2つのサイコロ」という表現が良く出てくることになります。
ただ、この「区別するしない」という考え方はとても大切なので覚えておきましょう。
「リンゴを配る問題と人間を配る問題の違い」であったり「A~Fの6人を3つのグループに分けました」といった問題で再度登場する考え方です。(別記事で解説します)
今回は中学受験場合の数の、「大小2つのサイコロ」というテーマでお話しました。
また続きをやります!
下のにほんブログ村のリンクから、中学受験の指導法・勉強法ブログのランキングを確認できます。(算田も参加しています。)
にほんブログ村
質問・相談・お仕事の依頼はこちらのメールアドレスへどうぞ
小学生であれば学年・成績は問いません。
sandasuutarou3.14@gmail.com
