今回は中学受験で出題される場合の数の1分野である、同じものを含む順列について解説してきます。
特に公式に含まれている割り算がなぜ割るのか、割る意味に焦点を当てていきます。
同じものを含む順列(重複順列)とは次のような問題です。
問題:A,A,A,B,B,Cの6枚のカードを一列に並べます。並べ方は何通りありますか。
この問題を書き出しではなく計算で求める方法を解説します。
先に結論を書いておくと、この問題の答えは60通りです。
そして多くのテキストの解答解説ページには下のような式が書いてあります。
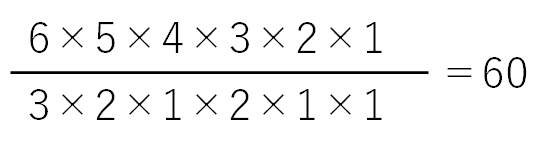
この式を見た小学生が、どのような意味でこうした式になっているのか一人で理解することは難しいですよね。
特に分母の部分、割る意味がどうしてこうなるのかわからないという声が多いです。
公式の丸暗記ではなく、なぜこのような式で求められるのか、その理由や背景を説明していきます。
順を追って説明しますので、一旦先ほどの例題は忘れましょう。最後にまた戻ってきます。
少し長くなりますが、お付き合いください。例題1~4の説明を読むことで、気づいたら先ほどの問題が解けるようになっています。(多分)
それではまず例題1から行きます。
例題1:A,B,C,Dの4枚のカードを1列に並べます。並べ方は何通りありますか。
まずはこちらの問題から行きましょう。
既に分かっている方は、例題1は飛ばしてもかまいません。例題2から読み始めてください
また、並び替えの問題を学習するのが全く初めてだという場合はこちらの記事からご覧ください。計算で求める方法を樹形図のアプローチから解説しています。
(関連記事:場合の数の解き方の本質は全部同じ。樹形図を簡単にしているだけ!)
この例題は色々な説明の方法がありますが、樹形図を卒業した子たちには「カード置き場」の説明をよく使います。

このように4か所のカード置き場があり、それぞれにカードを置いていきます。
一番左の1か所目に置けるカードの選択肢は、A~Dのどれでもいいので4通りです。
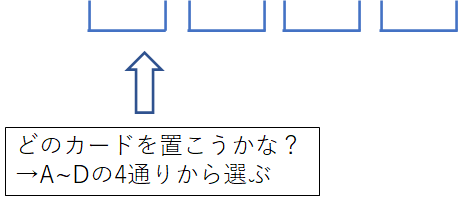
次に2番目のカード置き場を考えます。1番目で使ったカードは使えないので、それ以外の3通りから選びます。
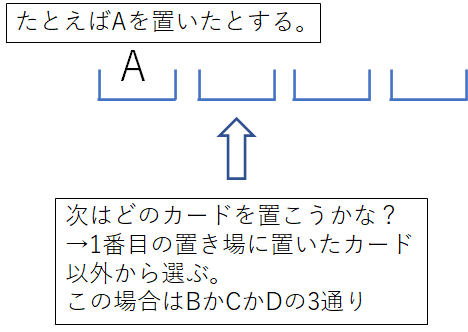
3番目のカード置き場は、下の図のように残った2枚から選ぶので2通りです。
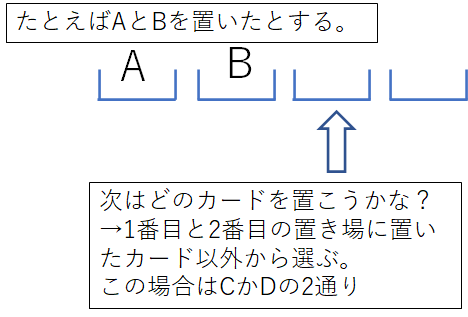
4番目のカード置き場は、残った1枚を置くだけなので選択肢はなく、1通りです。

これらの数字を全て掛け算して 4×3×2×1=24通り
が答えになります。 この問題は並び替えの基本問題です。次からが「同じものを含む順列」です。
問題2:A,A,B,Cの4枚のカードを一列に並べます。並べ方は何通りありますか?
先に答えを書いておくと、この問題の答えは12通りです。
解き方には様々ありますが、今回は、最終的に「a,a,a,b,b,c」の並べ方の説明をしたいので、それにつながる方法で解説します。
(もしもテストでこの問題が単独で出題された場合は、別の解き方で解いても全く問題ありません。)
さて、この問題を次のように書き換えてみます。
改題2:A,A,B,Cの4枚のカードを一列に並べます。並べ方は何通りありますか。
何が変わったのかというと、二つの「A」に色を塗りました。色を塗ることで二つのAに区別がつくものとして考えてみます。
説明の流れとしては
①まずは二つのAに区別がつくものとして計算してみる
②でも本当は同じものなので、後から「ダブっているもの」を調整する
こんな感じです。
さて、この改題の答えは24です。Aが色分けされて別の記号として扱われているので、例題1の「A,B,C,Dの並び替え」と全く同じ問題になりますね。
ですが今回は先々の説明のために、全通りを書き出してみます。

全て書き出すと上の図のようになるので、答えは間違いなく24通りです。
さて、これは二つのAに色を付けて区別がつくものとして計算したものですが、本当は同じAですよね。
では、この24通りの中には、いくつも同じものが含まれています。
例えば下の図を見てください。

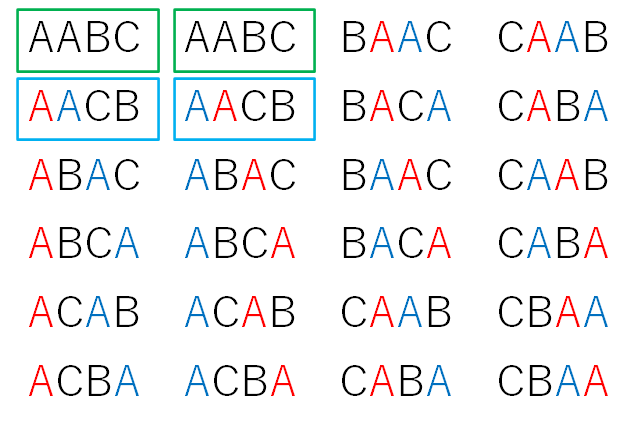
上の図の緑の枠で囲った2通りは、もし色がついていなかったら全く同じもので、区別がつきませんね。
下の図は色を消したバージョンです。色がなければどちらも「AABC」で全く同じものです。

同じようにして考えると、下の図の青い枠の2通りについても、色を消したら同じものになります。
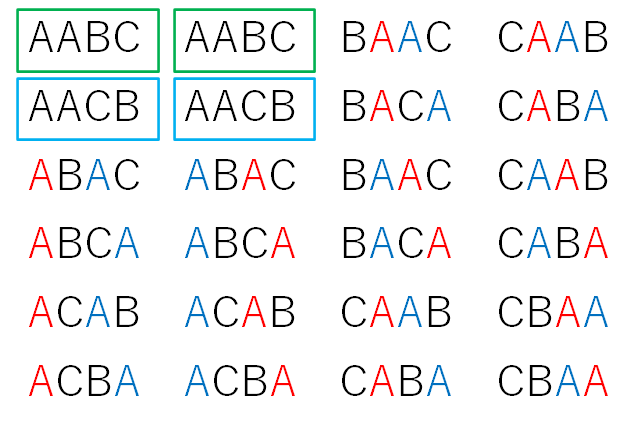
同じようにすべてのAの色を消していくと、下のようになります。
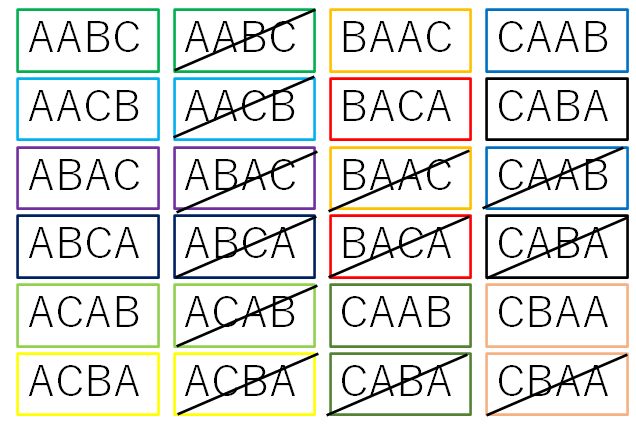
同色の枠で囲ったものが、同じ場合になります。
同じものの片方は斜線を引いて除外します。。
2通りずつペアで同じものが存在していますね。もともと24通りありましたので、 24÷2=12 より12通りが答えです。
例題3:A,A,A,Bの4枚のカードを並び替えます。並べ方は何通りありますか
さて今度は同じカードが3枚あります。この問題はどのようにして解いていきましょうか。
ちなみに答えは4通りです。この問題単体で考えた時の一番良い解き方は次のようなものでしょう。
カード置き場が4か所あり、先にBのカードをどこに入れるかを決める。4か所から自由に選べるから4通り。すると残ったところにAを入れればよいので、答えはそのまま4通り。
これで全く問題ありません。しかし今回は同じものを含む並び替えの説明の準備としての位置づけのため、別の方法で説明してみます。
(今から行う解説は、少し長くなります。繰り返しになりますが、この問題が単体でテストに出たとしたら、上で書いたような解き方で解くのがベストです。これから行うのはあくまで先の説明を行うための前準備です。)
これも例題2と同じように、色分けした問題をまず考えます。
改題3:AAABの4枚のカードを一列に並べます。並べ方は何通りありますか?
この問題も、もちろん答えは24通りです。ABCDの並び替えと同じことですから。
ではまず色を付けた状態で書き出して、ここから色を消していくことを考えましょう。
色分けして全24通り書き出したものが下の図になります。

この中で、緑の枠で囲まれている「AAAB」と同じものがいくつあるかを考えます。
すると、下の図の同じ緑の枠で囲ったものが同じ「AAAB」になります。
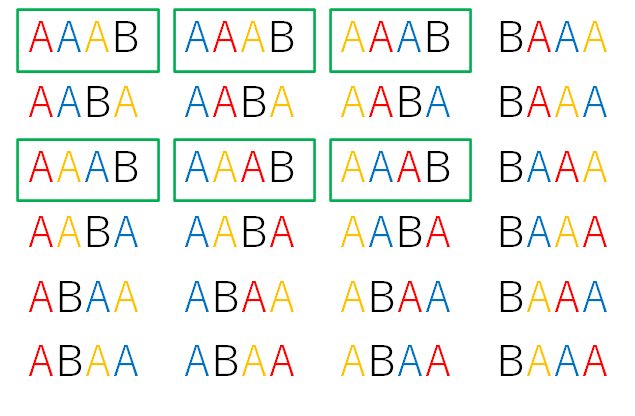
上の図から色を消したものが下の図になります。
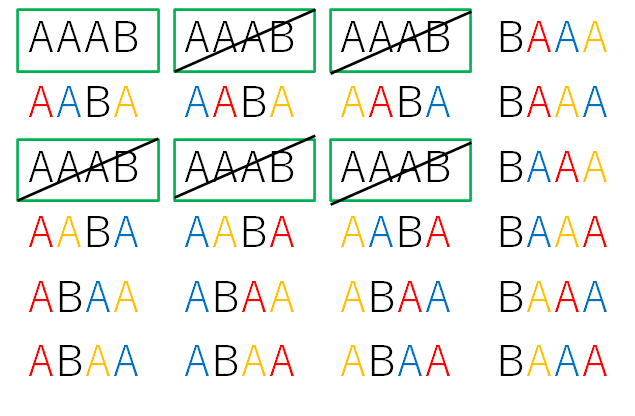
全く同じ「AAAB」で区別がつきませんね。
緑の枠で囲った6通りは同じものでした。斜線で除外しておきます。
同様に「AABA」と同じものを探すと下の図の紫の枠になります。
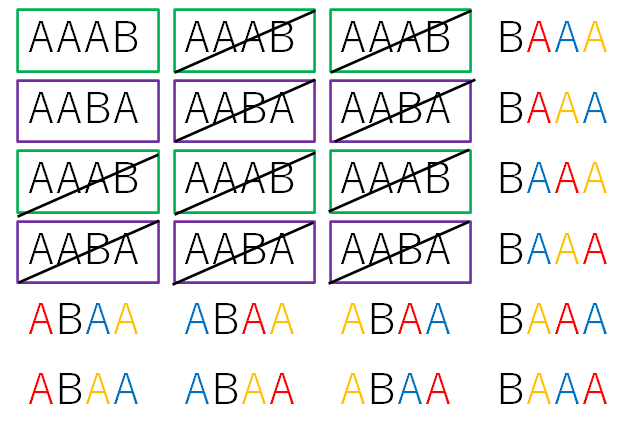
同様に残りのものについても枠で囲っていくと、下の図のようになります。
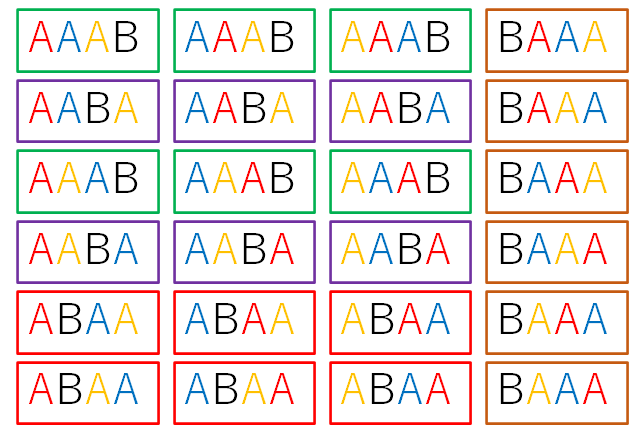
もともとはこうでしたが、色を消してみると
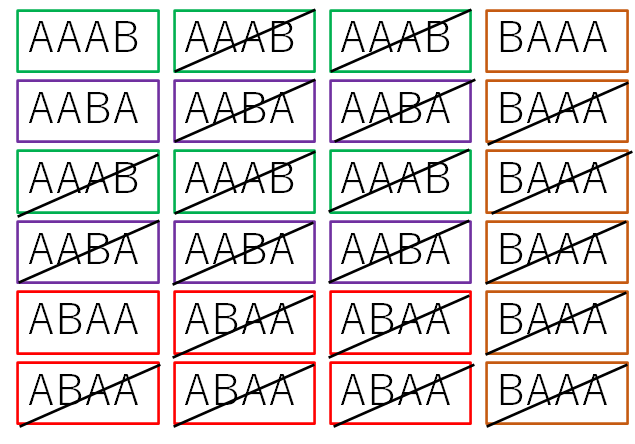
このようになり、結局は、枠の色が赤・緑・紫・茶色の4通りしか残りませんでした。
よって、「AAABを一列に並べるときの並べ方は何通りですか?」という問題の答えは4通りです。
もう少し深堀りしてみます。
上の図を見ると、4色の枠に分かれていますが、同じ色のものが6通りずつありますね。そのため、全24通りあるうち、それぞれ6個ずつダブりを持っているので、最初に求めた「24通り」の段階では、同じものを6回数えてしまっていたのです。
そのため、 24÷6=4 を計算し、答えは4通りと求めることができます。
この「÷6」の感覚はとても大切なのでしっかりと身につけましょう。同じものが3つあったら、÷6です。÷3ではありません。
その理由は言葉で説明するよりも、実際にこうして見せてしまうのが早いでしょう。
おまけ:この「同じものが6通りある」なのですが、最も格好良く式を書くならば「3×2×1=6」として求めます。 慣れてきたらここの順列も教えてあげたいですが、初めのうちは「同じものが3個あったら6で割るのか~なるほど~」くらいでも良いと思います。
例題4:AABBの4枚のカードを1列に並べます。並べ方は何通りありますか?
Aが2枚、Bも2枚になりました。
さてこちらも同じように、色分けして考えていきましょう。

AもBも色分けされていますので、片方ずつ見ていくことにしましょう。
まずはAの色だけを消してみます。(Bは色分けしたままにしておきます)すると、下の図のように同じものが現れます。
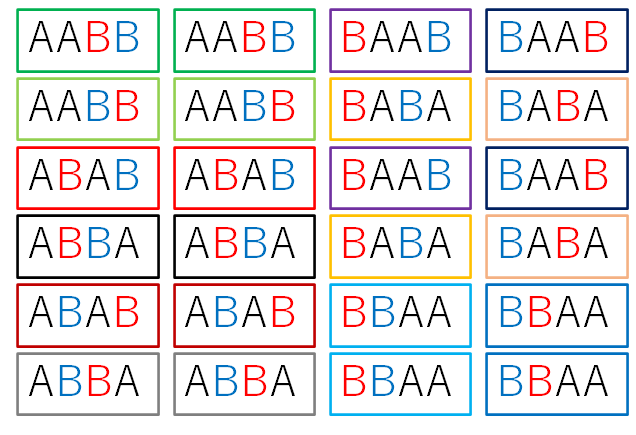
Aの色が消えると、2通りがペアになって同じものが発生します。同じものは斜線を引いて除外します。

最初の色分けした状態では24通りありましたが、Aの色だけ消した段階で
24÷2=12 の12通りに減りました。
さて次に、Bの色も消していきます。すると下の図のようになります。
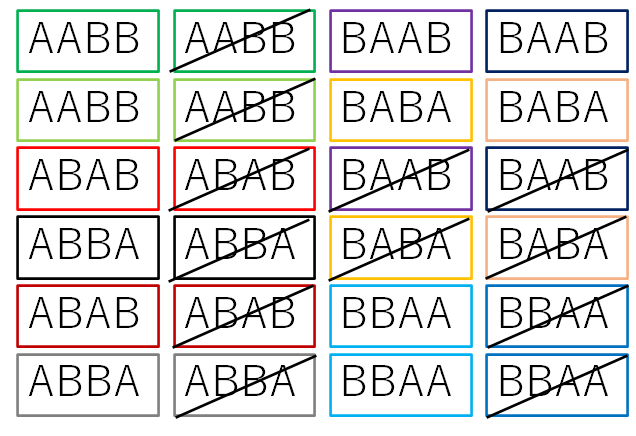
Bの色を消すことで新たに発生した同じものにも斜線を引いて除外していきましょう。
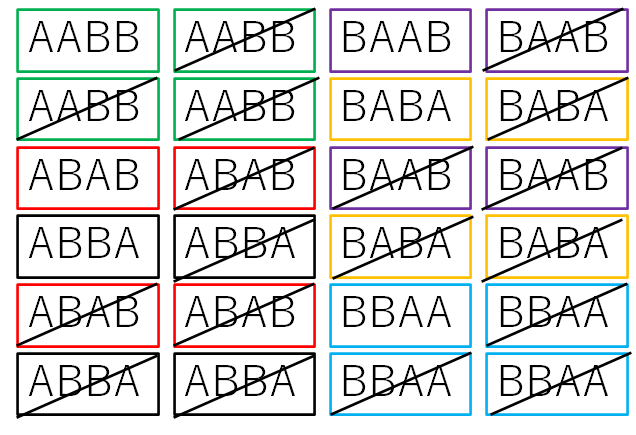
Aの色を消した段階で12通りにまで減っていましたが、Bの色も消すと、さらに2通りずつペアで同じものが発生するので
12÷2=6
となり、答えは6通りです。
さて、ここまでの説明を簡単にまとめます。
①まずは同じものも区別がつくとして、全部で何通りか計算する
②ダブっている数だけ割る。
同じものが2つなら 2×1=2 の2で割る。
同じものが3つなら 3×2×1=6 の6で割る。
③同じものを含むカードが2種類ある場合は、②の割る計算を2回行う。
ここまでで同じものを含む順列の基礎は説明し終わりました。
では冒頭の問題に挑戦してみましょう。
問題:AAABBCの6枚のカードを1列に並べます。並べ方は何通りありますか?
上で説明した手順の通りに考えていきましょう。
①まずは区別がつくとして計算します。
6枚のカードですので、「AAABBC」として考えます。つまり「ABCDEF」の並べ替え問題と同じです。
6×5×4×3×2×1=720 となります。
②・③ Aが3つ、Bが2つあります。Aが3つあるので 3×2×1=6 の6で割ります。更にBが2つあるので 2×1=2 の2で割ります。したがって式は
720÷6÷2=60 となります。
全てを一本の式にまとめ、最も「格好いい」書き方は次のようになります。
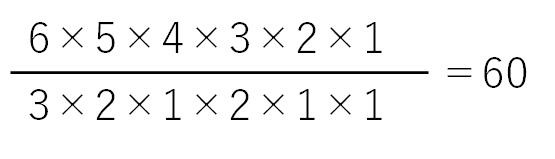
このようにすると1本の式にまとめられ、格好良くて美しい式になります。塾の回答冊子などではこのような書き方がなされることがあります。
(この辺りは美意識の領域なので、中学受験の記述回答を書く上ではここまでこだわらなくてOKです。また、分母は「3×2×1×2×1」でもOKです。数学的にきちんと一般化するならば、分母を「3×2×1×2×1×1」と最後に×1をつけた方が良いのですが、中学受験生はそこまでこだわる必要はないかなと思っています。)
以上が「同じものを含む並び替え」(重複順列)の考え方です。これを理解できると、例えば次のような問題を計算で求めることができます。
問題:AAABBBCCの8枚のカードを1列に並べます。並べ方は何通りありますか?
この問題の答えを計算することができます。素晴らしいですね。
全部で8個、Aが3個でBが3個、Cが2個ですので式は
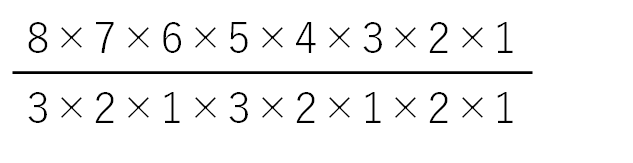
A3枚,B3枚,C3枚なので、分母は3~1と3~1と2~1の掛け算です。
このような式を書いて答えを計算することができます。答えは560通りです。
以上です!!!長くなりましたが終わりです!!!
小学生に重複順列を本質から理解してもらうためには、このくらい丁寧な導入をする必要があります!
塾のテキストの解答を読んで丸暗記しているだけでは、本当の意味での「分かった」にはなりません。
もしお子様がこうした問題で困っていた際は、この記事の解説を参考にお子様に説明してあげてみてください。
場合の数は、どんな目的で何を計算しているのかイメージを掴みづらい分野です。
この記事で紹介した方法は、少しでも目に見える形で、計算の意味を理解してもらおうと考えた方法です。
このような形で、直感的に意味を理解できるように指導していきたいと思っております。
関連記事:中学受験の場合の数・道順の基本全パターン攻略!書き出す解き方と計算で求める解き方と(今回の記事で解説した「同じものを含む並べ替え」の考え方を使って道順問題を解く方法を紹介しています。)
下のにほんブログ村のリンクから、中学受験の指導法・勉強法ブログのランキングを確認できます。(算田も参加しています。)他の先生の指導法ブログなども見てみてください。
にほんブログ村
2020年度中の家庭教師としての指導は可能な時間がかなり限られてしまいますが、キャンセル待ちやスポットでの指導でもOKという場合はご連絡ください。
小学生であれば学年・成績は問いません。
質問・相談・指導の依頼はこちらのメールアドレスへどうぞsandasuutarou3.14@gmail.com
