ミスが発生しやすいタイミングを、ランキング形式で第三位まで解説する記事を書いていました。
……がしかし!第二位の項目で筆が進みすぎてしまい、単独で一記事構成できる分量になってしまいました。
今回は第二位にランクイン予定の「二つ以上の動作を同時にやろうとしたとき」に絞って説明していきます。
第三位と第一位は、別記事で解説します!
第三位 問題文を読んだ直後
別記事で解説予定
第二位 二つ以上の動作を同時にやろうとしたとき
抽象的な表現になってしまいますが、「二つ以上の動作を同時にやろうとしたとき」です。
例えば 8/7÷2と3/2 のような計算です。(活字で帯分数がうまく書けないので、間に「と」を挟んでいます!)
この計算は「帯分数→仮分数」の処理と、「割り算→分母分子をひっくり返して掛け算」の二つの処理を行う必要があります。
このように二つの動作を頭の中で同時に処理しようとする際にミスが起こる確率が跳ね上がります。
もう少し複雑な事例も見てみましょう。
思考と記憶と計算を同時に行おうとするようなケースです。
例えば、下の画像のような問題を考えます。この問題を全て暗算で解こうとすると、どのようなミスが発生するのか……
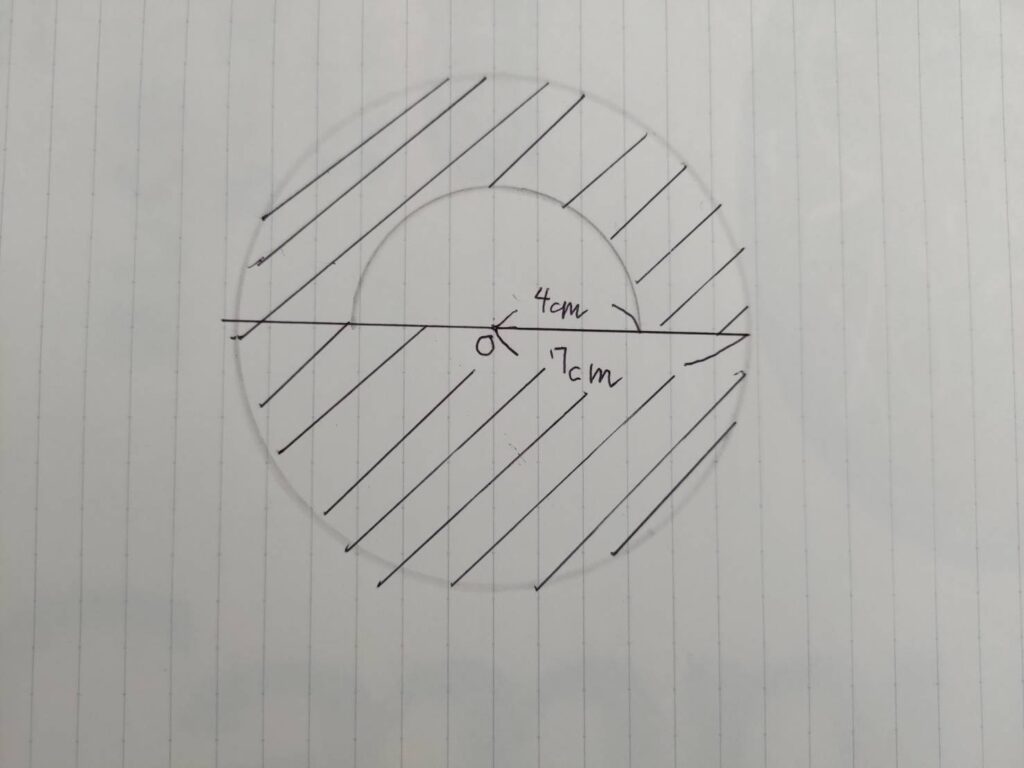
まずは方針を立てるための「思考」です。この場合は
「半径が7㎝の円の面積から、半径4㎝の半円の面積を引けば良いな!」のように方針を立てます。
次が計算です。
「半径が7の円だから、7×7×3.14=49×3.14だ」
そして記憶が必要になります。
「この49は覚えておいて、あとで引こう」これ以降は、49という数字を記憶しながらの計算になります。
そして再び思考です
「次は半径4㎝の半円だから、4×4×3.14÷2だ」
そして計算が始まります。
「4×4÷2=8 だから、8×3.14だ」
ここで、先ほど記憶していた49という数字を引き出します。
「49-8=41。だから答えは41×3.14だ!」
こんな流れで答えまでたどり着きます。
さて、一連の頭の動きを文字化してみましたが、ご覧になっていかがでしょうか!
率直な感想は「危険すぎる!!!!」ではないでしょうか?
問題の難度としてはさほど難しいものではありませんが、これをミスなく頭の中で解き切るのはなかなか難しいです。
その理由は、思考・計算・記憶の3種の頭の使い方が次々に切り替わっているからです。
人間の頭はおそらく、異なる種類の動作を同時に行うことが苦手にできています。
「記憶しながら計算」や「思考と計算を交互に繰り返す」のように、頭の使い方の切り替え回数が多ければ多くなるほどエラーが発生する確率が上がるのだと思います。
ミスを防ぐためには、異なる動作を同時に行わないことや、交互に繰り返すようなことを出来るだけ避けるのが有効です。
よく「途中式を書きなさい」という指導がありますが、その目的の一つはこれです。
方針を立てるための「思考」と、実際の「計算」を切り離したいのです。
こういう筋道でやれば答えが出るな、と方針を立てるのと、実際に筆算して計算するのとでは頭の使う部分が異なります。
そのため、思考した結果のメモとしての「途中式」を書き、その後は計算に専念する体制を整えるのが、式を書く目的の一つです。
第一位 答えが分かった! と思った直後
別記事で解説予定
まとめ
少し急ぎ足ですが、ミスが発生しやすい状況第二位を解説しました。
第一位と第三位については別記事で解説したいです。記事を書く時間を確保せねば……。
第二位のもっと具体的な対応策も、近いうちに詳しく書きたいと思います。
ミス対策は決して気合と根性ではありません。注意力でもありません。
技術と方法論で解決していきましょう!