速さと比の指導法公開

速さと比の解き方・指導法についての中心となる指導法を公開します。

算田にとってのとっておきのようなものなので、公開してよいものかどうか悩みました。
が、同業者が真似できるものならやってみろ！　の精神で公開することにしました。

速さと比の問題の構造

速さと比には3種類の比がある

当たり前の事ではありますが、速さと比の問題には3種類の比があります。
速さの比、時間の比、距離の比です。

算数の問題では、これらの比を変換することで解いていきます。
例えば「AとBの速さの比が2：3です」という問題文があったとします。これに続けて
「AとBがどちらも1時間進みました。進んだ距離の比の比は何：何ですか？」という問題があれば、答えは2：3です。速さの比を距離の比に変換しています。
「AとBがどちらも学校から駅まで行きました。かかった時間の比は何：何ですか？」という問題があれば、答えは3：2です。速さの比を時間の比に変換しています。

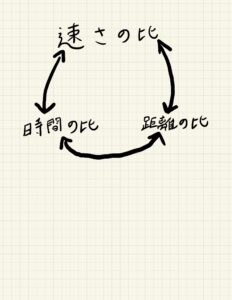
速さの比、時間の比、距離の比のイメージは、下の図のように相互に変換可能な関係をイメージします。
問題文で与えられた比を、他の比に変換することで問題を解き進めていきます。

比の変換を行う理由

速さの問題で比の変換を行う理由は、作問側の都合を考えると分かります。
比の変換を行わないと、簡単すぎて問題が成立しないのです。

「AとBの速さの比は2：3です。Aの速さは時速20㎞です。さてＢの速さは時速何㎞ですか？」→時速30㎞。では、簡単すぎて問題として成立しません。
「ＡとＢの速さの比は2：3です。ＡとＢが家から学校まで歩いたところ、Ａは30分かかりました。Ｂは何分歩くと学校まで着きますか？」→20分。
となると、少しは速さと比の問題っぽくなったでしょう？

このように、速さと比の問題として成立させようとすると、どうしても「比の変換」という手順が必要になります。（ここが速さと比の問題の醍醐味ともいえます）

速さと比を解く3手順

速さと比の問題を解く際の手順を3つに整理しました。
下の画像です。

手順①が　問題文にほぼそのまま書いてある比を見つける　です。
例えば、問題文中の「Aさんは時速20㎞、Bさんは時速30㎞」や「Aさんは20分、Bさんは30分歩きました」のような部分です。

手順③が　他の比に変換する　です。
速さの比が2：3の時に、時間の比3：2に変換するような手順です。

ここでは手順②はまだ空欄にしてあります。
さて、空欄の手順②は何なのか？という説明の前に、先ほどの比の変換の説明で、一つ隠れた前提条件を作っていたのにお気づきでしょうか？

先ほど例として挙げた
「AとBの速さの比は2：3です。AとBがどちらも学校から駅まで行きました。かかった時間の比は何：何ですか？」→答えは3：2
という問題。
よく三流の指導者は無配慮に「速さの比と時間の比は逆比！」と教えますが、これには隠れた前提条件があります。

「距離が同じ」という事です。AもBも二人とも「学校から駅」という同じ距離を歩いているので、時間の比が速さの比と連動しています。
これが仮に「Aさんは学校から最寄り駅まで、Bさんは東京駅から青森駅まで行きました」であれば、時間の比は3：2には決してなりませんよね。

同じように「AとBの速さの比は2：3です。Aは1時間歩き、Bは3日間歩きました。進んだ距離の比の比は何：何ですか？」という問題であれば、答えは決して2：3にはなりません。
時間が違うのですから当たり前です。

さて、ここで空欄にしていた手順②を発表します。
手順②は「一定のものを見つける」（同じものを見つける）です。

時間が同じ、距離が同じ、速さが同じ、のいずれかの一定を見つけることが手順②です。
ここで強調したいのは、手順②が先にあってその結果として手順③だという事です。

問題文に書かれた比を見つけたら、「どっちの比に変換しようかな？」と考えるのではありません。
「残った二つのうち、どっちかが一定のところがないかな？」と探してほしいのです。
一定が見つければ、自動的に残った一つの比に変換すれば良いだけです。

ここは思考のトリックのようなもので「どの比に置き換えようかな？」と考えるよりも「同じものはないかな？」と考え、消去法で残った比に変換したほうが答えにたどり着ける確率が上がります。
「どっちの比に置き換えるべきか」という抽象的な問いよりも「同じものはないか」という問いの方が具体的で考えやすいことが理由です。

よってまとめると
①問題文にほぼそのまま書いてある比を見つける
②残った二つの比の中から、同じものを見つける
③残った一つの比に置き換える

が速さと比の問題を解く際の思考手順です。

実際の問題で手順の利用例

3つの手順の次のポイントもあるのですが、一旦それは置いておいて、実際の問題でどのように使うのかを見ていきましょう。

まずは手順①、問題文にほぼそのまま書いてある比を探します。
すると、「いつもは15分」「今日は12分」と比になりそうな条件が書いてあります。ここから
いつも：今日＝15分：12分＝5：4
という時間の比が求められました。

次に手順②一定のものを探します。
時間の比は既に求められていますので、残った速さ又は距離のどちらかが同じになっていないかを探します。
すると、いつもも今日も、どちらも家から学校までという同じ距離を歩いていることが見つかります。
（速さは今日の方が早いので、一定ではありませんね）
よって手順②の「同じものを探す」は距離の一定が見つかりました。

最後の手順③です。
問題文で時間の比が書いてあり、距離が一定ですので、これを速さの比に置き換えます。
いつも（速さ）：ある日（速さ）＝4：5
となります。

ここまでで手順の①～③は終了です。
後は「今日はいつもより分速20m早い」という条件から、いつもと今日の速さの比の差である①＝20m/分として
いつも＝80m/分
今日＝100m分

と求められます。後は計算するだけですね。
80×15＝1200
（又は100×12＝1200）　より答えは1200mです。

このように手順①～③を使うと考えやすくなります。

手順3の次に位置するポイント

さてお待たせしました。
手順③の次の手順として書かれるものは……

「和か差を利用する」です！

今回の例題では、速さの差である4：5の差の①を利用しました。

というのも、これも作問側の都合が大きく関ります。
手順③までは終わった段階で、何かしらの比が求められています。例えば「AとBの速さの比が4：5」のような形です。

ここから問題として成立させるための方法は、大きく分けて4つあります。
1.　AとＢの比は4：5です。Ａの速さは分速80mです。Ｂの速さは？　→分速100m
2.　AとBの速さの比は4：5です。Bの速さは分速100mです。Aの速さは？　→分速80m

しかし、この二つは問題として味気ないです。簡単すぎます。
なので、次の2パターンが多く見られます。

3.　AとBの速さの比は4：5です。BはAより分速20m早いです。Aの速さは？　→④：⑤の差の①が20m/分なので、④は80m/分。答えは分速80m
4.　AとBの速さの比は4：5です。AとBの速さの和は分速180mです。Aの速さは？　→④：⑤の和の⑨が180m/分なので、④は80m/分。答えは分速80m

この2パターンの方が、入試の問題っぽくなっていますよね。
パターン3と4の方が「和と差を利用する」という観点から問題の山場を一つ多く設定でき、面白い問題になっています。

以上の理由から、手順①～③の後に続く解法としては
「和か差を利用する」（ことが多い）

です！体感として、速さと比の問題の95％は、和と差の考え方をどこかで利用します。

実際の問題での利用例2＜応用問題編＞

さて、速さと比の問題の「難問」とは何が難しいのでしょうか。
簡単に言えば、手順①～③＋「和と差の利用」のどこかで、条件を分かりにくく隠すことで難しさを演出しています。
最もよくあるのが手順②の一定の発見の所で隠すテクニックです。

下の問題をご覧ください。

まず問題を一読しただけでは、何が起きているのか状況を把握しづらいですよね。
ここで用いられる技法が「作図」です。

速さの作図には大きく分けて「状況図（線分図）」と「ダイヤグラム」があります。
今回は状況図の方を書いて考えてみましょう。

下の画像のような図が書けます。

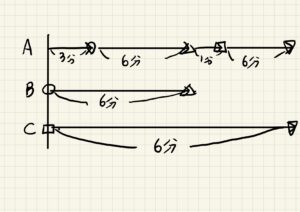
まずはAとBの速さの比を求めたいと思います。
問題文で書かれている条件は、ほとんどが「時間」の条件です。
という事は「問題文にほぼそのまま書かれている比」は時間の比だろうと予想することが出来ます。

すると、何かの一定を探す必要があります。AとBの速さが異なることは明らかですので、今回は「距離一定」を探します。
AとBが同じ距離動いている箇所はないかという視点で探すと……

出発地点～BがAに追いついている所まで（△マークの所）　という一定の距離が見つかりました。
Aが3+6＝9分かけて移動した距離を、Bは6分で移動しています。

ここから、AとBの（同じ距離を進むのにかかった）時間の比＝3：2→速さの比2：3　と変換できました。

同様にAとCの比も求めていきます。
AとCが同じ距離移動している「距離一定」という視点で探すと……
やはり、出発地点～CがAに追いついた地点　という距離一定が見つかりました。

Aが3+6+1+6＝16分かけて移動した距離を、Cは6分で移動しています。
AとCの時間の比＝8：3→速さの比は3：8
と求められました。

あとは連比の要領で、A：B：C＝6：9：16　と求められます。

この問題では、手順②の「一定の発見」のところで、作図による可視化をしないと発見が非常に難しくなるように問題が書かれています。

よって作図の目的は「一定がどこにあるか気づきやすくするため」です。
作図が嫌いなお子様も、作図の目的を説明してあげることで納得してくれることが多いです。

作図のルールも、一定が発見しやすくなるようにという観点から決めています。
まとめの前に、旅人算の線分図（状況図）の書き方についての記事のリンクを貼っておきます

まとめ

速さと比の問題を考える際の指針となる事とその指導法を解説しました。
今回紹介した内容は、特定の問題にのみ使えることではなく、速さと比の問題に広く一般的に適用できる考え方です。

私自身が問題を解く際に無意識に行っていた動作を、子供にもわかりやすく言語化したものになります。
個々の問題の解き方の指導ではなく、全体を通した考え方の枠組みの指導法です。
指導方針にもあるように「解説冊子の0行目」にあたる内容です。

この方法・考え方はこれ自体がすごいのではなく、この考え方を使って長期間トレーニングを行うことで体に思考手順が染みつき、しばらくした頃に結果が出てくるような性質のものです。
様々な問題を同じ考え方で思考して解くことを繰り返し、理論を実践できるように鍛えていきます。
生徒の思考スタイルを徐々に正しい方向に導いていくようなものです。
そのため、ブログ読者の保護者や同業の方に参考にしていただける部分もあると思いますが、本来は「1：1で即時アドバイス可能な指導状況」で真価を発揮します。

算田がどういった指導法で授業を行うかは出来る限りブログで公開します。
その指導法を使ってどのようにお子様とトレーニングするのかは、その子の理解の進み具合や性格・思考のタイプによって異なるので、場合分けが多岐にわたります。

理論はブログ上で公開できますが、実践の方法はブログだけではなかなか伝えきれません。
算田の指導法にご興味ある方はLINE公式又はメールよりご連絡ください！