別解を覚えようとしなくて困る子が続出！【容器と水量】

小5算数の一番の難所は、間違いなく比です。これは5年生の後半に習う塾が多いです。
SAPIXや早稲田アカデミーでは5年生の後半に習います。

では5年前期で最大の難所は何なのか？　という質問に、私は「容器と水量」と答えたいです。
その理由は、ひとつの解法を覚えただけでは通用しなくなる単元だからです。

つまり複数の解法を覚えて問題によって使い分けるという初めての経験だからです。

容器に水が入っていて、そこに重りを入れるような問題には、大きく分けて3つの解法があります。
このうち、1つは誰でも覚えていて、1つは多くの受験生が大好きでよく使うようになり、そして1つを軽視しがちです。
詳しく説明していきます。

今回の記事は保護者向けの解説です。問題の詳細な解法というよりは、容器と水量という単元がどのように構成されているのか、受験勉強全体でどこに位置する問題なのかといった視点からの解説を試みます。

算数が得意な読者の方は、どのような解法があるのか是非じっくり読んでください。
算数が得意でない読者の方は、解説の部分はとりあえず流し読みして、記事の後半だけ読んでください。

※最近はあまり時間が取れずブログの更新間隔が空いてしまっています。図は電車内でipadで作ることにしたので、電車の揺れにより文字と線が一部歪んでしまっています。許してください。

パターン①　おもり全沈みパターン

ひとつ目の解法は、おもりが水の中に全て沈むような場合です。

例題

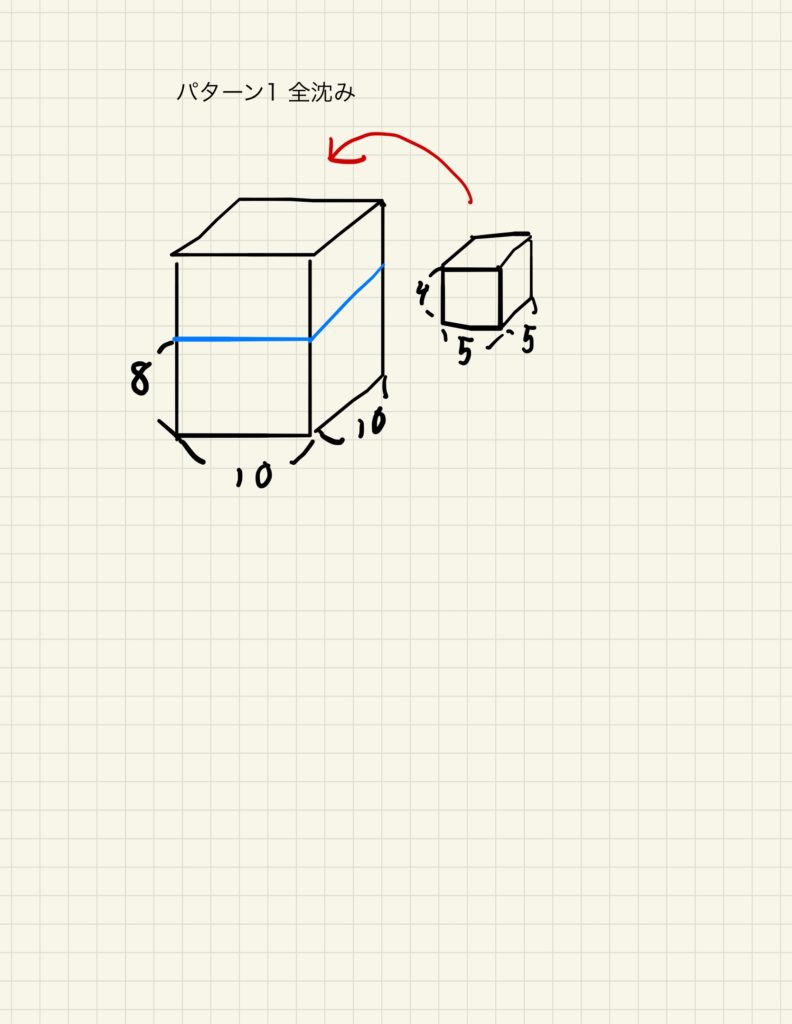
この問題は最も簡単なパターンです。
この場合は、重りの体積と同じ体積の水が増えたと考えて計算します。
重りの体積は　5×5×4＝100㎤　なので、100㎤の水が増えた場合の水位の変化は
100÷（10×10）＝1㎝　より、1㎝深くなりますので、答えは8+1＝9　の9㎝です。

これは最も簡単なパターンですので、これ単体ならば多くのの受験生が理解できています。

パターン②　柱が突き抜くパターン

二つ目の解法は、重りの頭が水面から出ている場合です。
つまり重りが全て水に沈んでいるわけではなく、一部は水面から出ている状態です。

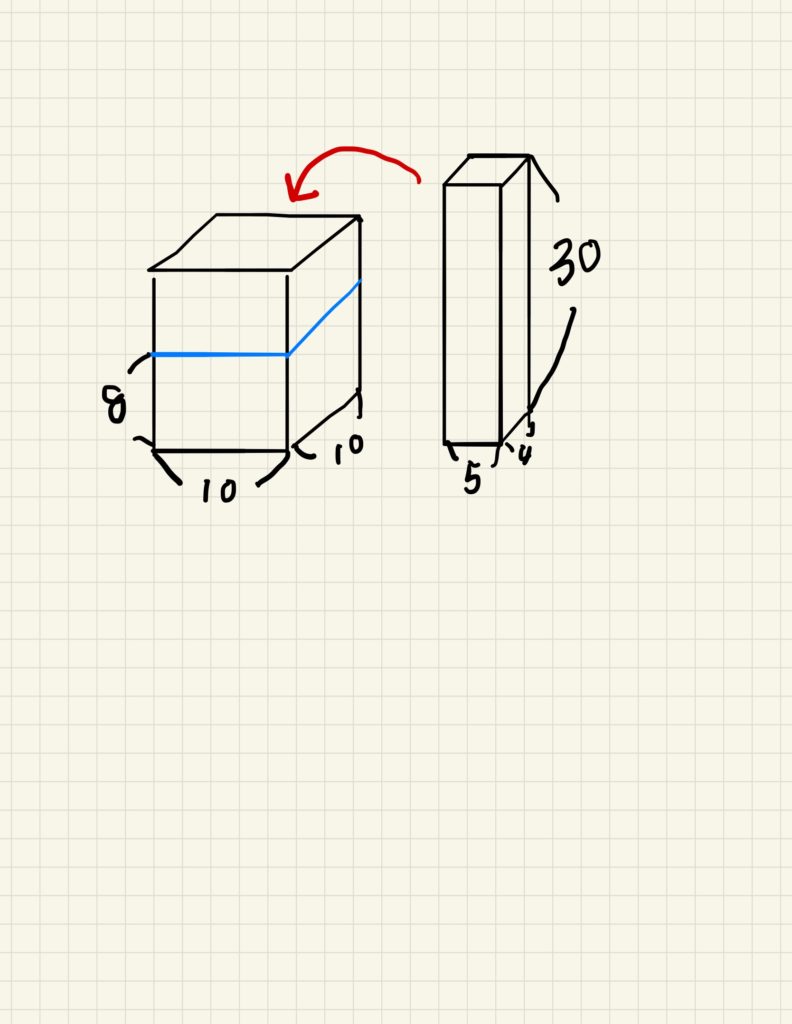
この問題は、重りの高さが30㎝と非常に高いので、水面から飛び出す形になります。
パターン①とは異なる解法を使う必要があります。
キーワードは「底面積が減る」です。

水の入った容器に重りが差し込まれると、重りの底面積である　4×5＝20㎠　の部分には水が浸入できなくなります。
このことを「容器の底面積が100㎠→80㎠に減った」のように考えます。　（保護者向け記事のため細かい説明は省略します）

よって、解答の方針としてはまず水の体積を求めます。
10×10×8＝800㎤

この水が、底面積80㎠の容器に入れられると考えます。よって　800÷80＝10㎝　が答えとなります。

重りが入ったことにより、計算上の底面積を変化させて考える解法です。
後半で詳しく説明しますが、このパターン②を受験生は最も軽視しがちです。

パターン③　横から見た面積図を使うパターン

パターン③は、重りが動くようなシーンで有効な解法です。
「重りを入れたところ水の深さが□㎝上がった」や「入っていた重りを水から外に出したところ水面が□㎝下がった」というような問題です。

この問題の解法として一般的なのは、下のような図を書いて求める方法です。

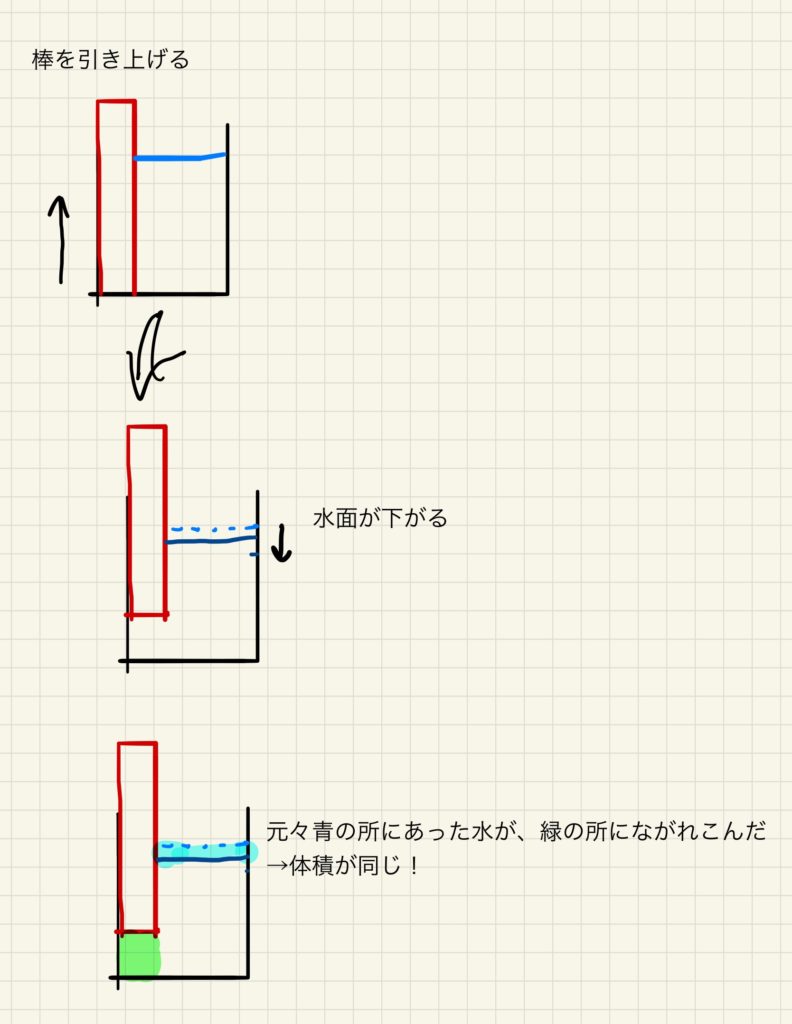
細かい部分は分からなくても大丈夫です。とにかくこのように図を書く方法があります。
図を書く→水が移動した部分の体積が同じ
であることを利用して解いていきます。

3つの内どれが一番おろそかになりやすいの？

さて、ここまで読んできてどうだったでしょうか。中学受験経験者の方は「当然最初から知っていたよ！」となるかもしれませんが、そうでない方が初めてこの記事を読んだ際の感想を予想してみます。

解法①　なるほど分かった
解法②　分かった……ような？
解法③　図だ！なんだかすごそう。覚えよう！

子供たちもこれと同じ反応をします。
①は大体みんなすぐに理解して、②はよく分からない状態で③の解法の説明をされると「これはすごい！　覚えよう！」となります。
図で解くというのはイメージ抜群です。印象に残ります。

さて今回の記事の趣旨としては　解法②の底面積の変化として解く方法を忘れてはいけないよ！　ということです。
図で解く方法は印象に残りやすく、システマチックに解けるので多くの生徒が好んで覚えます。
そして幸か不幸か、③の面積図の解法だけ覚えていれば、②を理解しないままでも結構な数の問題が解けてしまうのです。
5年生の標準問題くらいであれば②でも③でもどちらの解法でも解ける問題が多いので、ひとつの解法しか覚えていなかったとしても、症状が顕在化しません。
しかし今後学習が進むにつれて、ひとつの解法しか使えないというのは必ず足枷になります。

何で一つの解法しか覚えたがらないの？

「３つの解法があるから、３つとも覚えよう！」で記事を終わりにしても良いのですが、せっかくなのでもう少し深掘りしてみます。
どうして1つの解法しか覚えない子が続出するのか？　という疑問を考えていきます。

新4年生から受験勉強を始めたとすると、この容器と水量の単元に出会うまでは、ほとんどの単元で「一つの問題に一つの解法」で済んでいたのです。
これまでの受験生の成功体験としては「解法をひとつ覚えれば問題が解けるようになる！」と強烈に印象付けられています。

しかしここから先は「複数の解法がある中でどれを使うかの選択」が技術として必要となります。その切り替えの入り口にあたる単元なのです。
ですから、ここで過去の成功体験を一度捨てなければなりません。
一種類の武器だけで倒せる問題はここまでで、ここから先のダンジョンでは何個もの武器を使い分けないと倒せない強力な問題が待ち受けています。

このことに気づけないまま、過去の成功体験にとらわれたまま、一つの解法にこだわって学習を続けてしまうと、必ず成績が落ちていきます。
「4年生までは成績が良かったのに、5年生から少しずつ成績が落ちていった」というケースの約半数はこの「複数解法という新しい状況への順応」でつまずいている印象です。（ちなみにもう半数は「比と割合」でつまずいています）

まとめ

第一の結論としては「容器と水量の問題には大きく分けて3種類の解法があり、全て覚えないと後々困ることになる」です。

しかし第二の結論としては「子供が一つの解法にこだわってそれ以外を覚えることを拒否するのは、過去の成功体験があるから」です。

このことを意識しないままに「覚えなさい！」と言っても反発を招きます。
受験生がいままで勉強してきたことと、これから勉強することを見通したうえで、生徒が今どの立ち位置にいるのかを意識しながら接していくことで、指導者の助言が聞き入れられやすくなります。

受験全体を見通した指導とよく言いますが、このように子供の心理にも配慮して指導してあげると、うまくいきやすいのではないかと思います。
良ければ参考にしてください。