目次
時計算の落とし穴
時計算が分からない!
という子に、時計算の解説をしても響きません。
実は分からない原因は旅人算に埋まっています!!
……とここまでは、ちょっと良い参考書や授業で言ってくれます。
確かに時計算って旅人算の特殊なものなので、考え方は一緒です。
しかし、それを説明しても算数が苦手な子が「分かった!!」とはなりません。
より一層「うーん……」となってしまいます。
ここに算数が得意な先生と、苦手な生徒のギャップが存在します。
算数が得意な先生が無意識にスルーしてしまっている部分で生徒は決定的に困っています。
算数の得意な先生が意識できていない考え方とは何なのか?
何を教えてあげれば生徒は理解するのか?
具体的にどんな指導方法を用いれば、無理なく理解が進むのか?
順を追って解説していきます。
時計算ってどんな問題?基本を把握
まずは時計算とはどのような単元なのかを把握しましょう。
下の図解画像をご覧ください。
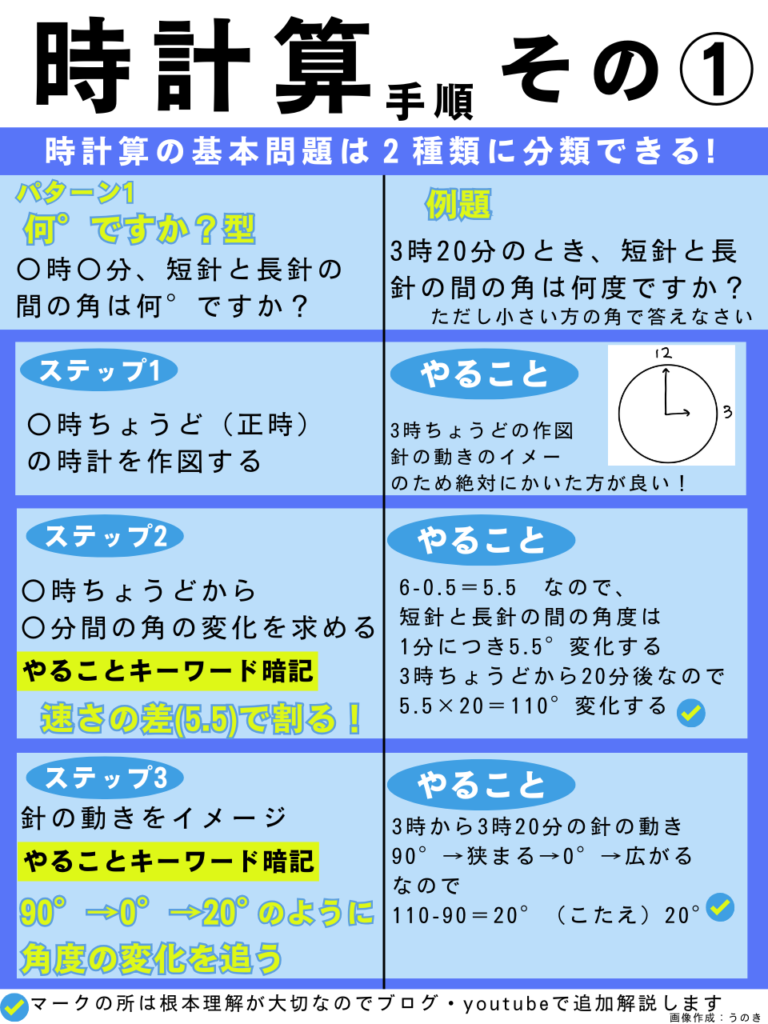

時計算の基本問題は大きく分けて二種類です。
簡単に言うと「〇時〇分の時の角度は何度ですか?」と「〇°になるのは何時何分ですか?」です。
問題の型は基本的に二種類しかなく、解き方も決まり切っています。
(応用問題になると、角度を二等分する問題など型にはまらない発展問題もありますが、一旦それらの応用のことは置いておきます。時計算を始めて習った子の困りごとを解消することを目的に記事を書いていきます!)
出題のパターンが少ないので、こう思う方もいるかもしれません。
「解き方を暗記してしまえばいいのでは?」
実はこれが落とし穴。
算数講師の中にも「時計算なんて解き方を覚えればいいだけじゃん」という方針で指導している方が多いように思います……
図解の右側で簡単な解き方を紹介しています。これを覚えれば解決するかというと……そうでもないのです。
「☑」マークを付けた箇所は、子供からすると理解しにくい部分になります。
算数が得意な人からすると「何が分からないのか分からない」となるのですが、子供が理解できない原因があります。それは何なのでしょうか?
どのような指導をすれば理解できるようになるのでしょうか?
一つずつ解説していきます。
時計算、何が難しいの?
次の段落から、具体的な指導法の解説に入っていきます。
この段落では、時計算の何が難しいのかについて説明していきます。
一般的な時計算の解説では、どうしても理解できるようにならない子が大勢います。
その「つまずきポイント」を解消するための指導法を次の段落から解説しますので
まずは、一般的な解説では何が難しいのか? を知っておくとより深く理解できると思います。
※お時間のない方はこの段落は飛ばして、次の「分からない原因①追いつきの旅人算の「速さの差で割る」の本質を理解していない」から読んでいただいても大丈夫です!
例題で解説
例えばこんな問題。
【例題】
3時から4時の間で、短針と長針の間の角が30°になるのは3時何分?
【解法】
時計の長針は1分で6°、短針は1分で0.5°動く。 ★1
よって1分間では6-0.5=5.5 より、5.5°ずつ間の角は変化していく。 ☆2
3時ちょうどの時は90°離れているので
間の角が30°になるのは
90-30=60 の60°変化したときと
90+30=120°変化したときの2回存在する。 ☆3
よって答えは
60÷5.5=120/11=10と10/11分 ★4
120÷5.5=240/11=21と9/11分
こんな感じの解説になります。
一見すると、普通に分かりやすい解説に思えるかもしれません。
算数が得意な保護者の方からすると「これ以上何を説明すればいいの?」
と思われたかもしれません。
次の段落で説明していきます。
この解説のどこがイマイチなのか?
一般的な解説はこんな感じです。
そして、よくある「丁寧な」解説では★1と★4の箇所が手厚く解説されています。
つまり
★1長針と短針の角速度に関連する部分。長針は60分で時計を一周するから360°動く。だから1分だと6°動くよねー
のような解説と
★460÷5.5=120/11に関連する部分。時計の針で旅人算をしていると考えようねー
のような解説です。
大人が聞くと分かりやすい解説なのですが、算数が苦手な子供にはいまいち響きません。
子供が困っているポイントは実は別の箇所なんです。それが☆2と☆3です。
☆2 1分間では6-0.5=5.5 より、5.5°ずつ間の角は変化していく。
☆3 90-30=60 の60°変化したときと90+30=120°変化したときの2回存在する。
この二か所です。
普通の解説書・塾の授業では「もちろんこうなるよね~」という感じでサラッと言われてしまいますが、実はここが分かっていない子が多いです。
この二か所を突き詰めて指導・解説することが今回の記事で紹介したい指導法の核であり、次の段落から詳しく書いていきます。
分からない原因①追いつきの旅人算の「速さの差で割る」の本質を理解していない
子供たちの理解状況
時計算という単元は、必ずその直前に「速さ」や「旅人算」という単元を学習するようにどの塾もカリキュラムが組まれています。
繰り返しにはなりますが、時計算とは旅人算の一種なので、本質的には今までやってきた内容と同じです。
今までは「分速〇m」だったのが「分速〇°」になるだけ……
だと思っている講師が多すぎます!!
違うんです。子供が躓いている原因は全く別のところにあります。
まず状況を整理しましょう。
どの塾でも、時計算の直前には旅人算を学習しています。
その旅人算の中ではこんな問題が解けるようになっています。
例題
AさんとBさんは240m離れたところに立っています。
Aさんは分速50m、Bさんは分速20mで歩きます。
AとBが同時に同じ方向に向かって出発します。
AがBに追いつくのは出発してから何分後ですか?
この問題はこんな風に解きます。
240÷(50-20)=8分
さて、この単元をサラッと学習した後の子供たちの理解状況はこんな感じです。
「追いつきの時は、距離の差を速さの差で割る!」
確かに正しいのですが、なぜ距離の差を使うのか?なぜ速さの差で割るのか?
計算の意味までは納得できていないことが多いです。
実は……時計算では、この本質が理解できていないといつまでも解けるようにならないという恐ろしい単元なのです。
(逆に言えば、旅人算の本質が理解できているならば「なーんだ簡単じゃん」と言う生徒もいます)
速さの差を本質的に理解するための方法「旅人算を表で求める」
「速さの差で割る」という行為の本質を理解するための方法として、「旅人算を表の書き出しで求める」という方法があります。
本質を理解するための方法は、いつも泥臭い力技です。スマートには指導できません。パワーです。パワー!
例題をもう一度掲載します。
例題
AさんとBさんは240m離れたところに立っています。
Aさんは分速50m、Bさんは分速20mで歩きます。
AとBが同時に同じ方向に向かって出発します。
AがBに追いつくのは出発してから何分後ですか?
この問題をこんな風に解いていきます。
まずスタートした時点では、二人の距離は240mですよね。
では1秒後の距離は何mでしょうか?
Aさんは50m追いかけて、Bさんが20m逃げているので、30m縮まりますよね。
なのでこのように票に書きます。
| 何秒後 | 0 | 1 | |||||||
| 距離 | 240 | 210 |
こんな感じで、追いつくまで表を書き続けていきます。
| 何秒後 | 0 | 1 | 2 | 3 | 4 | ||||
| 距離 | 240 | 210 | 180 | 150 | 120 |
この辺りで「あ!30ずつ減ってるんだから÷30で求められるじゃん!」と気づけるとベストです。
気づけていない子には、このタイミングで講師からアシストを出します。
「これ、なんか規則はないかな? 計算で求められんかな?」
のような感じです。
1秒につき30mずつ距離が縮まっていくので、240mの距離をゼロにするためには
240÷30=8秒後 と求められることが分かります。
これが旅人算の追いつきの公式の意味なんだよーと教えてあげると
「なーんだそういうことだったのかー」と納得している様子をよく見ます。
塾の集団授業だと、計算の意味までゆっくり理解している時間は取れないのかもしれませんね。
短時間でたくさんの問題を習得するのも大事ですが、今紹介したような根本の意味の理解を大切にする授業も良いのではないかな?と思ったりします。(話がそれましたね💦)
ちなみに表を最後まで書いたらこうなります。
| 何秒後 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 距離 | 240 | 210 | 180 | 150 | 120 | 90 | 60 | 30 | 0 |
よって8秒後に二人の距離がゼロになっているので、追いつくのは8秒後。
分からない原因②追いつきの旅人算の「距離の差」の本質を理解していない
追いつかない旅人算
上の段落で使った、旅人算を表で求める方法を利用して指導します。
くどいかもしれませんが、念のため問題を再掲します。
| 出発から何秒後か | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 距離 | 240 | 210 | 180 | 150 | 120 | 90 | 60 | 30 | 0 |
では、この表を見ながら考えてみてください。
問題
AさんとBさんの距離が30mになっているのは何秒後ですか?(すべて答えなさい)
どうでしょうか。
表を見れば、7秒後に二人の距離が30mになっていることが分かりますね。
なので「7秒」は答えの一つです。
実はもう一つ答えがあります。
それは何秒後なのでしょうか?
更に表を書き続けていきます。
| 出発から何秒後か | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 距離 | 240 | 210 | 180 | 150 | 120 | 90 | 60 | 30 | 0 | ??? |
8秒後に追いつきが発生し、そのさらに先、9秒後はどうなっているのでしょうか?
AさんがBさんを追い抜いて、さらに先に行っているはずですよね。
Aさんは50m/分、Bさんは20m/分なので、30mずつ離れていくはずです。
なので、表はこうなるはずです
| 出発から何秒後か | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 距離 | 240 | 210 | 180 | 150 | 120 | 90 | 60 | 30 | 0 | 30 |
9秒後にも再び30mになっていますよね。なので9秒後も答えです。
よって問題の答えは 7秒後,9秒後 となります。
では次に、この問題を計算で求める方法を考えていきましょう。
(小学生に指導する際は、計算で求める方法だけではなく、書き出しで実際に「やって見せる」ということが大切です。頭の中で理解するだけではなく、実際に目で見て納得するという行為の効果は大きいです)
ここで出てくる考え方が「距離の差」です。
ついに登場しました。大ボス「距離の差」です。
まずは最初の「7秒」の方を計算で求める方法を考えます。
最初のスタート時点では240m離れていました。これを、30mの距離にまで近づけたい訳です。
ということは……210m近づければいい! 240-30=210 の、210m近づけたい。
1分につき30mずつ近づいていくんだから、210÷30だ!
この発見が出来るように、指導で導いていきます。
同様に、2回目の30mである9秒後の求め方についてもやっていきます。
2回目に30mになるのは、一旦距離がゼロになって、追い越してさらにその先のこと。
240mの距離が一旦ゼロになって、さらに30m引き離すということは……
240÷30=8秒
30÷30=1
8+1=9秒
こんな式を考える子もいるかもしれません。
これも間違ってはいないのですが、さらにもう一歩先まで学べるようにしましょう。
「240m近づく」&「30m引き離す」ということは、合わせて270÷30で計算できる。
ここまで納得できるように指導の中で導きます。
ということでまとめです。
求め方としては
(240--30)÷30=7分
(240+30)÷30=9分
時計算に応用する
上の二つの段落「分からない原因①」と「分からない原因②」で学んできたことを利用すると、時計算が一気に理解しやすくなっているはずです。
算数が苦手な子は、おそらく今までは「速さの差で割る」という行為のことを「追いつきの旅人算の時に使うおまじない」くらいにしか思っていませんでした。
それが、表で書き出して答えを求めた経験によって「距離が1分ごとに変化していくから速さの差で割るのか」という本質を理解できるようになりました。
また、「距離の差を使う」ということもなんとなく「追いつきの時は距離の差なんだよね」くらいにぼんやりとしか思っていなかった子も、なぜ距離の差を利用して計算するのかが理解できるようになっているはずです。
この状態で、やっと時計算を学習する下地が出来ました。
正直、ここまでの道のりは長いです。
仮に90分の授業で時計算を指導しようと思ったら、ここまでで60分は使っています。
でも、下準備として前提の理解・共有をしっかりやってから応用の指導を開始すると、応用問題は一瞬で理解できたりするのが算数の面白い所です。
基礎は大事。古からの言い伝えは守るべきですね。
さて本題に戻ります。
念のため問題を再掲しておきます。
【問題】
3時から4時の間で、短針と長針の間の角が30°になるのは3時何分?
ここまで理解できた子には、次のように解説します。
まずは図を書きます。
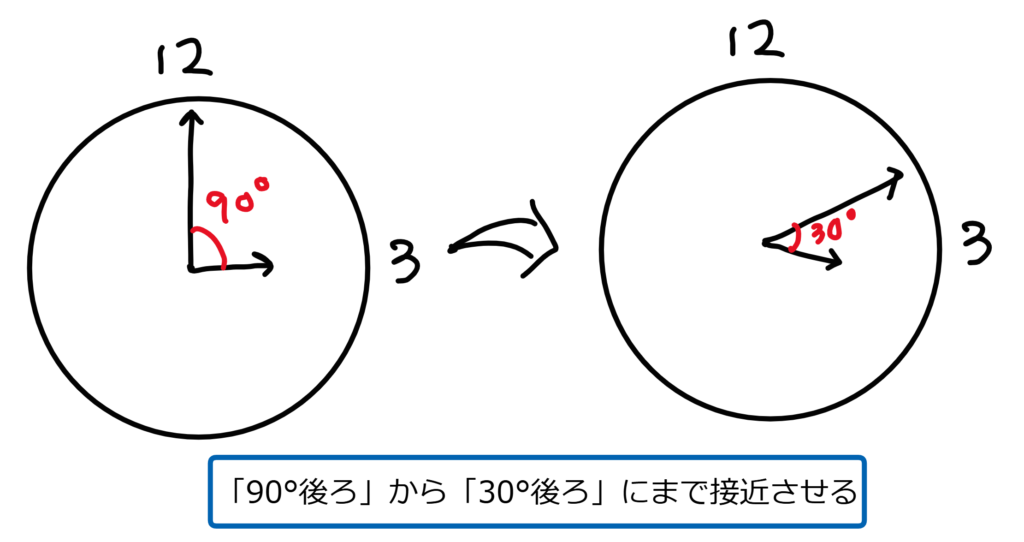
次に、表を書いて書き出しで求めようとしてみます。
| 秒後 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 短針と長針の間の角 | 90° |
出発した時点では90°離れています。
では、1分後はどうなるでしょうか?
長針は6°追いかけて、短針が0.5°逃げますので、5.5°縮まりますね。
表にするとこんな感じです
| 秒後 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 短針と長針の間の角 | 90° | 84.5° |
同様にして、どんどん書き出していきます。
| 秒後 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 短針と長針の間の角 | 90 | 84.5° | 79° | 73.5° | 68° |
さて、問題ではこれが「30°」になる瞬間を求めたいのですよね。
ということは、90°からスタートしているので、90-30の60°分、縮めたいことになります。
なので……5.5°ずつ小さくなっていって、60°小さくしたいので
「あ! 60÷5.5だ!!」
これが気づければ授業は完了です。
これに自分で気づけた子は、時計算の計算が「角度の変化÷5.5」で求められるということが心から納得できます。
この後で、別パターンの問題も同様に指導するのですが、そこは割愛します。
ここまで理解が出来た子にとっては、もう別パターンでも同じ問題に見えていることでしょう。
まとめ
時計算の問題が理解できない本当の原因について解説してきました。
ふたつの原因とは
①「速さの差で割る」の本質が分かっていない
②「距離の差」の本質が分かっていない
のふたつでした。
どちらも旅人算の単元で学習する内容ですが、実は旅人算の基礎問題を解くだけなら、あやふやな理解のままでも乗り切れてしまいます。
そのあやふやさが露呈するのが時計算。ということで、漠然と「時計算が苦手だ」と感じる子が多いのですが、原因は旅人算です。
時計算の表面的な解説・解法で満足せず、しっかりとコアの部分まで学習出来た子には、確実な学力が身につきます。
このようにしっかりと後に残る勉強を続けていきたいですね。
保護者の方がご家庭で指導する際の参考になれば幸いです。