算田がこれまだに書いてきた、解法や算数の技術論に関する記事をまとめます。
算数解き方・解説の方法を言語化した記事です。
算田の指導方針の基本的な部分としては
・解法の暗記ではなく、根本原理を心から理解する
・教えてもらって分かるのではなく、一人で解けるようになるための方法
・できるだけシンプルな考え方で
です。
この記事は以下のような方を対象にしています。
・算数の問題に興味のある保護者
・同業者の算数講師
・算田へ家庭教師依頼を検討している方 算田の指導方針を知りたい方
立体の切断
立体切断の切断面の形の見分け方は、ほとんどの指導者は見た一発のセンスで指導指定ます。
誰でもできる論理的な方法を紹介します。
立体の切断・長方形の見分け方編
-
-
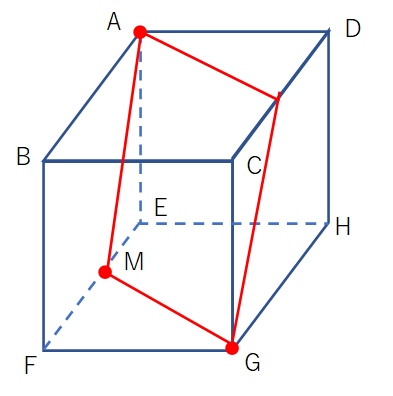
立体切断の切り口「これひし形なの?長方形かと思った」の解き方・長方形の見分け方編
この時期の6年生は立体の切断の問題によく出会います。 切断面の形を問う問題があります。切断面は長方形なのか? ひし形なのか? 平行四辺形なのか? この辺りの解き方は、ほとんどの塾では指導されていないの ...
続きを見る
立体の切断・ひし形の見分け方編
-

-
立体切断の切り口「これひし形なの?長方形かと思った」問題の解き方・ひし形の見分け方編
前回の記事では、立体の切断面が長方形なのかどうかを見分ける方法・解き方について説明しました。今回はこの続編で、ひし形かどうかを見分ける方法・解き方につて説明していきます。さて、ひし形とはどのような形で ...
続きを見る
平面図形・立体図形
こちらもCHECK
-
-
平面図形と比の解説、「やってることは分かるが自分で気づける気がしない!」の解決方法
平面図形と比の問題の考え方を紹介します。平面図形と比の問題で一番多いお悩みは「解説冊子に書いてあることが正しいのは分かるけど、なんでそれを思いつくのか分からない!」ではないでしょうか。 平面図形の問題 ...
続きを見る
こちらもCHECK
-
-
丸暗記じゃない!円すいの中心角の公式が成り立つ証明!
「公式を憶えろ!とにかく暗記だ! 理屈は良い。丸暗記じゃ~」という旧石器時代の教育方法みたいなものがいまだにまかり通っていたりします。 最終的には公式として暗記したほうが良いものはありますが、かといっ ...
続きを見る
場合の数
場合の数は、意味も分からず解法の暗記に走りがちです。
お子様が「これは割るんだっけ?割らないんだっけ?」とか「5C2だから10だ」のように言っているのなら危険信号です。
根本から理解しておかないと、後々大変なことになります。
こちらもCHECK
-

-
場合の数の解き方の本質は全部同じ。樹形図を簡単にしているだけ!
今回は場合の数の解き方・考え方について解説していこうと思います。結論から言うと、中学受験の基本を学ぶ段階では樹形図を重視します。場合の数を苦手としている子は本当に多いです。その原因の一つは、場合の数が ...
続きを見る
こちらもCHECK
-

-
中学受験の場合の数・道順の基本全パターン攻略!書き出す解き方と計算で求める解き方と
中学受験の場合の数で特徴的な出題である道順問題について解説していきます。道順の問題には大きく分けて2つの解き方があります。書き出していく解き方と、計算で求める解き方です。初めのうちは、書き出していく解 ...
続きを見る
こちらもCHECK
-

-
【場合の数】「大小2つのサイコロをふります。何通り?」サイコロの大きさが変わると答えが変わる!?【中学受験】
今回は中学受験における場合の数、サイコロ問題を扱っていきます。サイコロ問題にも「割るの?割らないの?」という疑問が付いて回りますので、その辺りを解消していきたいと思います。 突然ですが問題です。問題1 ...
続きを見る
こちらもCHECK
-
-
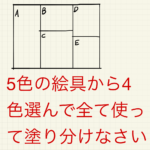
一見同じでも解法が全然違う!場合の数・5色から4色選んで全て使って塗り分けなさい
今日は久しぶりに解説記事を書いていきます。場合の数の色塗りの問題です。今回の記事は以下に当てはまる方に読んでいただきたいと思います。①お子様に算数を教えている保護者の方②5年生までは得意だったはずの単 ...
続きを見る
こちらもCHECK
-

-
場合の数と現実世界を結び付けるには?入試には出ない単元「確からしさ」の存在意義。
突然ですが皆様に問題です。 AからEまでの5人を一列に並べます。ただしAとBの2人は両端のどちらかに並べることとします。並べ方は全部で何通りありますか。 いかがでしょうか。みなさま、この問題を考えよう ...
続きを見る
グラフの読み方
算数が得意な人が無意識にやっているグラフの読み方を、可能な限り言語化した記事です。
自信作です。是非お読みください。
こちらもCHECK
-
-
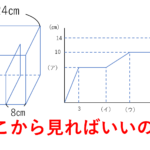
【シリーズ算数が得意な人には何が見えているのか】グラフの読み方編
新シリーズ【算数が得意な人には何が見えているのか】をはじめます。このシリーズでは、算数が得意な人の頭の中を徹底解剖していきます。算数が得意な子は一瞬で見てることが、苦手な子は何時間かかっても見えない。 ...
続きを見る
速さ・旅人算
速さと比の問題を解けるようにする指導は、算田が最も自信がある分野の一つです。
指導法を文章で表現するのが難しい単元なのですが、可能な範囲で言語化しました。
是非ご覧ください。
こちらもCHECK
-

-
速さと比の指導法公開
速さと比の解き方・指導法についての中心となる指導法を公開します。 算田にとってのとっておきのようなものなので、公開してよいものかどうか悩みました。が、同業者が真似できるものならやってみろ! の精神で公 ...
続きを見る
こちらもCHECK
-

-
旅人算「比を使って解く」って説明は抽象的すぎないか?もっと具体的に説明したい【算数が得意な人には何が見えているのかシリーズ】
旅人算の問題は、6年生になるとほぼ全てが比を使って解く必要がある問題になります。 塾の先生の解説などでよく使われるワードに「比を使って解く」というものがあります。 このような抽象的な説明では、苦手な子 ...
続きを見る
狂った時計!
-
-
狂った時計でこんな図は使うな! 解法・解き方紹介
「狂った時計」というジャンルの問題があります。この問題で、一部の生徒(早稲アカ生に多い)が、おすすめできない図を使って考えていることがありますので記事にしてみました。後半では算田おすすめの方法も紹介し ...
続きを見る
規則性・数の性質
こちらもCHECK
-

-
【日暦算】書き出し!カレンダー問題必殺の解法【何曜日ですか?】
中学入試ではカレンダーに関係する問題が出題されることもあります。例えば次のような問題です。 問題 ある年の10月2日が金曜日のとき、翌年の2月1日は何曜日でしょうか? こうした問題、テキストには次のよ ...
続きを見る
こちらもCHECK
-

-
N進法って何?【保護者向け解説】
今日はN進法について解説していきます。大人でも理解しづらい単元である「N進法」を保護者の方向けに解説してみます。今回は「N進法とは何か?」という視点で記事を書きます。 そもそも「私たちが普段使っている ...
続きを見る
-

-
参考N進法は何が難しいのか?&簡単な解法【中学受験】
N進法という単元があります。2進法や3進法などです。例えば2進法とは「0,1」の2つの数字だけで数を表す方法で、2進法で「1110」と書くと10進法(普段私たちが使っている数字)では14を表します。N ...
続きを見る
こちらもCHECK
-

-
いもづる算割る版
続きを見る
こちらもCHECK
-

-
「~で割ると〇余る」系の問題。気合根性&計算で解く!
約数と倍数の単元にで頻出の「~で割ると〇余り、~で割ると〇余る」系の問題を3パターンに分けて解き方を解説します。例えばこんな問題です。 「4で割ると2あまり、6で割ると3余る整数を小さい方から3つ書き ...
続きを見る
こちらもCHECK
-
-
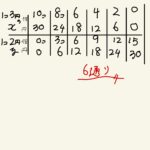
【芋づる算】便利な方法は捨てよう!泥臭く解こう!
世の中便利なものに溢れていますが、便利でハイテクすぎると仕組みがよく分からなくなります。自転車がどう動いているのかは見れば大体分かりますが、自動車がどういう仕組みで動いているのかは素人では分かりません ...
続きを見る
割合
こちらもCHECK
-
-
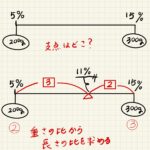
食塩水の「てんびん図」って何だ!?なんで濃度がてんびんで解けるの??
今回は食塩水の濃度計算を、てんびん図を使って解く方法を解説します。 食塩水の問題で登場する図というと、ビーカー図(コップの形をした枠の中に、%、食塩水の重さ、食塩の重さの3つの情報を書き込むもの)と面 ...
続きを見る
指導の心がけ
こちらもCHECK
-

-
問題読み飛ばしを防ぐには!? トレーニング方法!
今回は算数の文章題での読み飛ばし・読み間違いを防ぐ為のトレーニング方法をご紹介します。 文章の読み間違いによるバツ、多いですよね。「あー!A地点じゃなくてB地点だった!」「AをBで割るか!逆にしてた! ...
続きを見る
こちらもCHECK
-

-
算数が超得意な子には何を教えるか?【カレーと肉じゃがの共通点】
算数が得意な子と苦手な子、どちらを指導することが多いかと聞かれれば、それはやはり苦手な子のほうが多いです。苦手科目の強化で家庭教師をつけるというご家庭が多いですよね。 一方で、算数が超得意なのでもっと ...
続きを見る
多くの「一般的な家庭教師」が陥りがちな罠……力のある講師が教えないと全く成長できない理由について
こちらもCHECK
-

-
何を考えれば良いのかすら分からない!を脱するためには?
目次1 考えたって分かるはずがない囲碁の問題2 算数の場合3 国語の場合 考えたって分かるはずがない囲碁の問題 考えるためには基準となる知識が必要である。そんな内容で記事を書いていきます。 突然ですが ...
続きを見る