世の中便利なものに溢れていますが、便利でハイテクすぎると仕組みがよく分からなくなります。
自転車がどう動いているのかは見れば大体分かりますが、自動車がどういう仕組みで動いているのかは素人では分かりません。
算数の問題の解き方を学ぶ際に、いきなり自動車のように完成された便利な方法から学ぶのではなく、まず泥臭い自転車のような方法から学んだ方が理解が進むのではないか。
そんなテーマについて書いていきます。
つまり、最も早く解けてスタイリッシュな解法が、子供にとってかならずしもベストだとは言い切れない。
多少遠回りでも、直感的に理解しやすく単純な解法から学んだ方が上達の役に立つのではないか?
そんなテーマです。
題材としては「いもづる算」を扱います。
目次
解法① 一般的な解法
芋づる算の例題と、多くの教科書に載っている「模範解答」を紹介します。
赤字にした箇所の手順は、最初に学習する段階では不要なのではないかと私が思っている箇所です。
問題:1本180円のユリの花と1本120円のバラの花があります。代金の合計が1800円になるように、2種類の花を買いたいです。花の買い方は何通りあるでしょうか?
どちらかの花が0本でも良いものとします。
よくある解説
①ユリの本数をx、バラの本数をYとすると
180×x+120×y=1800 となる。この式全体を最大公約数の60で割り、式を簡単にすると
3×X+2×y=30
となります。
この式を満たす整数の(x、y)の組を探すと下の表のようになります。
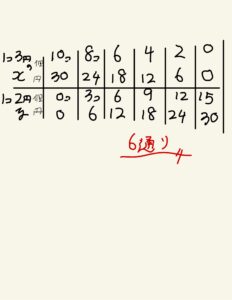
よって答えは6通りです。
解法② 「最大公約数で割る」は労力の割に簡単にならない.最初はやらなくて良い
次に、赤字で書いた手順を省略した解法を紹介します。
つまり、最大公約数で割るという事をしないまま表にして解いていきます。
手順は本土同じですが、青字の箇所が上で書いた解説と異なる部分です。
①ユリの本数を○、バラの本数を△とすると
180×〇+120×△=1800 となる。
この式を満たす本数(〇、△)の組を探すと下の表のようになります。

よって答えは6通りです。
いかがでしょうか? 解く際の面倒くささに、大した違いはありません。
最初に赤字で紹介した解法は、「最大公約数で割る」という大層な手順を踏んだ割に、その効果と言えば、180×Xの計算が3×Xになるくらいのものです。
別に180のかけ算だって受験生ならば難なくできます。そんなに嫌がるほどの物でもありません。
数字を簡単にしない方が、現実感がある
解法①の方は、予習シリーズに載っている物です。
四谷大塚や早稲アカではこちらの方法で習います。
解法①は、解法②をちょっと工夫して計算を簡単にしたものです。
解法②の発想が先にあり、それを発展させたものが①です。
確かに最大公約数で割ると数が小さくなり計算が楽なのですが、その代償として、何をやっているのか想像しにくくなります。
割らない状態のまま計算すれば「180円のモノが3個あるんだな」のように理解しやすいですが、割ってしまうと「3が3個……?」となります。
ほとんどの子にとって、最初から高度すぎる解法を教わるのは害が大きいと考えています。
初めてスキージャンプを体験する人に向けて、着地の際のテレマーク姿勢まで教えるようなものです。
最初は不格好でもいいから、とにかく出来るようになることが先決だと思います。
原始的な方法でまず覚え、十分に上達してから、計算の工夫が出来るようになる。こんな順序でも遅くはありません。
目安として、5年生で初めて芋づる算を学習する生徒で、算数の偏差値が四谷のテストで55を超えていないのであれば、原始的な方法で覚えた方が良いと思っています。
現6年生で、芋づる算数が苦手で復習している生徒も、最初は原始的な方法から覚えた方が理解しやすいと思います。
工夫は、一度困った後で教えるべき
入試算数の指導法は研究が尽くされていて、色々と良い方法が編み出されています。
最も早く効果的に解く方法があれば、模範解答にはその方法が記されます。
ただ……一度も困ったことがない人に、その「困り」を避けるための工夫を教えてもピンとこないことが多いです。
便利な方法と言うのは、その前に面倒で原始的な方法があり、その面倒を回避するために編み出されるものです。
いきなり最終形の解法を教えるのではなく、一回困ってみてから良い方法を教わった方が良いです!
結論:初学者は完璧な解法でなくてもいい。原始的な解法で良い
今回の結論はこれです。
最初にその単元を学習するときは、いきなり一番便利な解法で覚えようとしなくても良い。
多少遠回りでも、本質に近い方法で覚えて、その後で余裕があったら便利な解法を覚えるのが良い。
普段の算田の授業でも、その単元を最初に指導する際は、いきなり「答え」を示さないようにしています。
場合の数であれば全通り書き出しますし
規則性であれば表を20行でも30行でも書きますし
円すいの展開図の中心角の求め方は、なぜ半径/母線になるのか証明を一緒にやります。
そんな感じで、解法の仕組みを心から納得できるようになってから始めて、便利法則を教えるようにしています。
一見遠回りなようですが、結果的にこちらの方が遠くまで行けます。