文章題が苦手だったり、テストで少しひねった問題になると急に解けなくなるというお悩みのあるお子様の原因の一つかもしれない? と算田が考えていることを紹介します。
算数の問題では、設問文で問われている数値には直接つながらないものをまずは求めるという考え方が必要になります。
まずは簡単な例で植木算の問題で説明しましょう。
100mのまっすぐな道に、端から端まで5mおきに木を植えていきます。木は何本必要ですか?
→求め方:100÷5=20……「木と木の間」の数が20個なので、20+1=21本が木の本数
簡単に説明するとこんな感じです。この時、問題では「木は何本ですか?」と聞かれているのに、最初に求めたものは「間の数」である事に気づきましたでしょうか。
木の本数を求めるために、中間目標として「木と木の間の数」という数値を求めているのです。
4年生や5年生で「文章題が苦手だ」というお悩みをお持ちの場合、原因の一つとして考えられるのはこの中間目標の設定という意識がないことです。
最も初歩の文章題「4人の生徒に3個ずつリンゴを配りました。全部で何個ですか? →12個」であれば、問われていること最初に行う計算が直結しています。
しかし問題が複雑になるにつれ、設問で問われていることと初手の計算が乖離してきます。
そのために必要なのが中間目標の設定。つまり「Aを求めるためにはBが必要で、Bを求めるためにはCが必要だから、まずCを求める計算をやろう!」という意識です。
この感覚が自然に身に付くお子様であれば心配はいらないのですが、算数を致命的に苦手にしてしまっているお子様は、ここの意識で悩んでいることがあります。
なぜAを問題で聞かれているのにCを求めないといけないのか理解できず。仕方ないのでC→B→Aという流れを暗記して乗りきって、組み分けテストなどで少しひねった問題が出題された際に分からなくなって×が付きます。
保護者から見ると似たような問題のはずなのになぜかテストで急にできなくなる、という現象の原因の一つです。
一口に「文章題が苦手」と言っても、原因は様々あります。例えるなら体調が悪くて「おなかが痛い」となった場合に原因が様々考えられるのと同じです。
原因を特定して、解決するための対策をピンポイントで打たないと症状は良くなりません。
意外と気づきにくくて目立たないポイントですが、中間目標の設定というような意識を持てているか、確かめてみてください。
今回の記事で解説した「中間目標の設定」という発想を平面図形の入試問題に応用したものが下の記事です。 平面図形と比の問題の考え方を紹介します。平面図形と比の問題で一番多いお悩みは「解説冊子に書いてあることが正しいのは分かるけど、なんでそれを思いつくのか分からない!」ではないでしょうか。 平面図形の問題 ... 続きを見る
入試問題のように論理が複雑な問題でこそより威力を発揮する考え方です。
初歩の算数も入試レベルの算数も、根底に流れる大切な考え方は同じです。
良かったらこちらも合わせて読んでみてください。
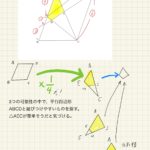
参考平面図形と比の解説、「やってることは分かるが自分で気づける気がしない!」の解決方法