平面図形と比の問題の考え方を紹介します。
平面図形と比の問題で一番多いお悩みは「解説冊子に書いてあることが正しいのは分かるけど、なんでそれを思いつくのか分からない!」
ではないでしょうか。
平面図形の問題の一般的な解説は結果論で書かれています。
まずとある相似に着目する→何か長さの比が求まる→図形の比が分かる→更に何か比が分かる→答えが出る
のような感じです。その手順で答えが出せるのが分かるけど、最初の一歩の「とある相似に注目する」は何でそこに注目したんだ!?勘か?超能力か!? と言いたくなることでしょう。
けっして超人的な勘で解いているわけではなく、解ける人はある思考法を使っているから解けるのです。
「ゴールから逆算して考える」という考え方を練習すると、自分で最初の発想にたどり着けるようになります。
出来る人は無意識にやっていることなので説明が省かれてしまうことが多いのですが、今回はその「算数が得意な人の無意識」を出来るだけ伝わるような形で解説しようと思います。
ブログの指導方針欄にも書かせていただいている「解説冊子の0行目」に通じる内容です。解説冊子の1行目の手前で、その背景となる思考を解き明かしてみたいと思います。
個々の解法やテクニックではなく、発想法や思考法、問題解決が上手な人はどのように考えているのか?という疑問を出来る限り言語化しようという試みです。
問題は2019年鴎友中学第一回の入試問題を題材といたします。
下の画像をご覧ください。
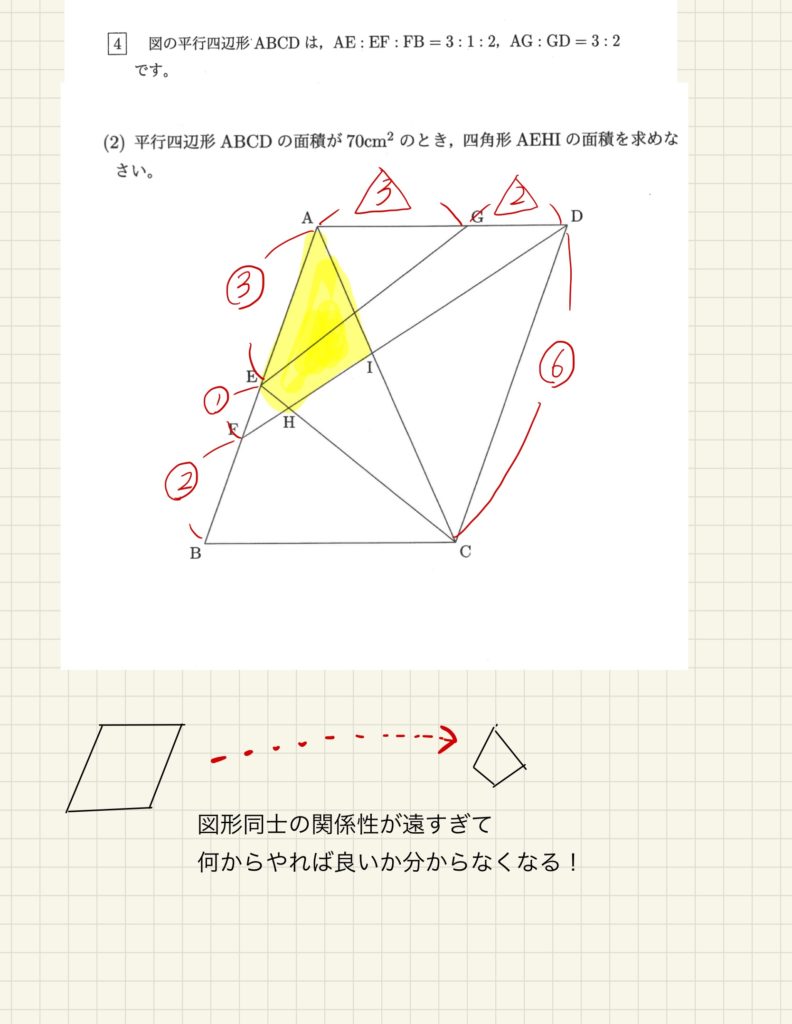
全体の平行四辺形と、黄色いマーカーで塗った四角形の面積の比が何:何なのかを求めれば答えが出せる問題です。
この両者の図形は「関係性が遠い」ので、面積が何:何なのかすぐに求めることは難しそうです。
「関係性が遠い」とは、比べる二つの図形(平行四辺形ABCDと四角形AEHI)が、「対角線で切っただけ」や「相似!」のような単純な関係になっていないという意味です。
どのような手順で、全体の平行四辺形とマーカーの四角形を結び付けていけばよいのでしょうか?
下の画像ごご覧ください。
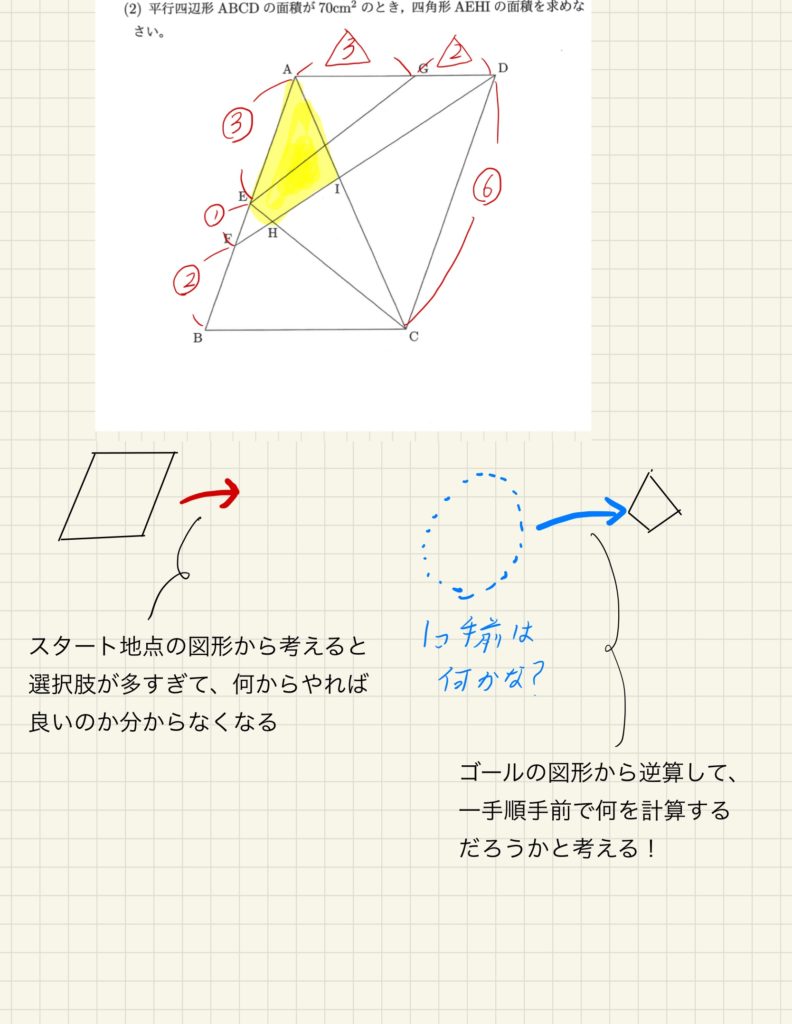
スタート地点である平行四辺形から考えると、可能性のある選択肢が多すぎて、何をすればいいのか分からなくなってしまいます。
△EBCを求めようか、△AIDを求めようか、△AFIか、△AECか、△ACDか……
やれることが多すぎて選べなくなります。
多くの受験生はここで手が止まって動けなくなっています。
そして解説を読んで「あ~AECだったのか~分かるけど気づけないや~」となっています。
そうではないのです。発想を切り替えましょう。ゴールとなる黄色マーカーの四角形から考え始めるのです。
黄色い変な形の四角形の面積が求められるということは、その直前はどのような流れで求められるのだろうか?と考えます。
これがゴールから逆算して考えるです。
下の画像をご覧ください。
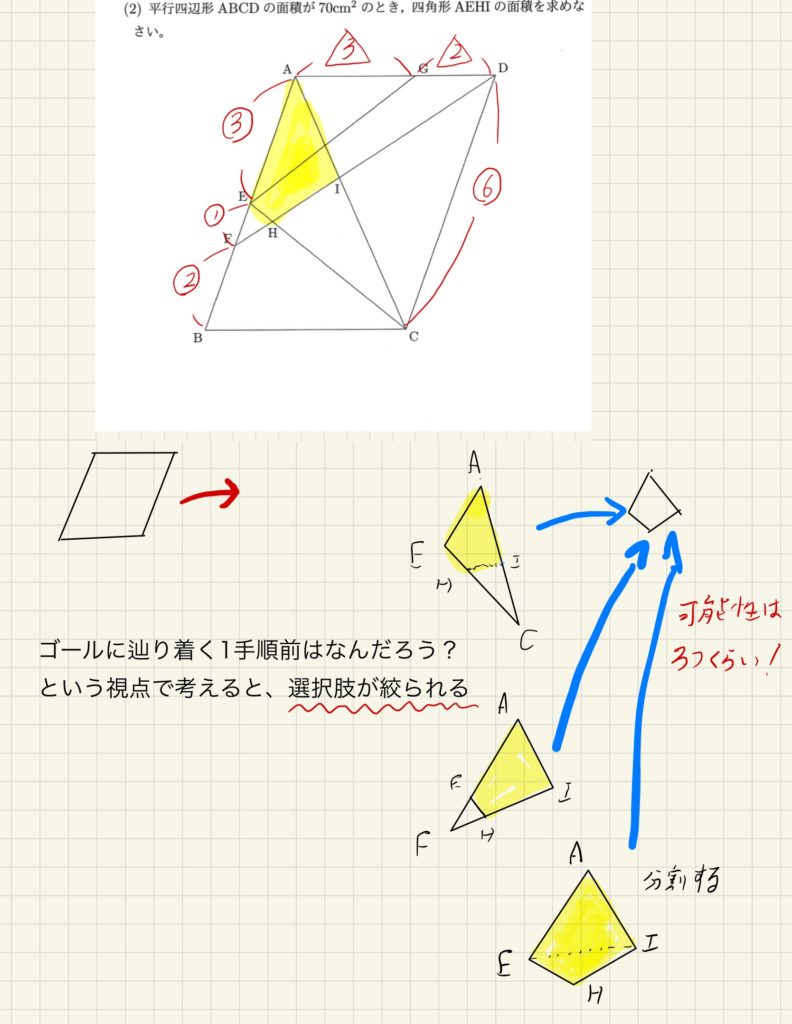
黄色マーカーの図形の面積を求めるために考えられる手段は大体3通りくらいかと思います。
①△AECを線HIで切り分けて求める方法。
②△AFIから線FHで切り分けて求める方法
③四角形AEHIを線EIで分割して求める方法
このくらいでしょうか。求めるべき黄色い図形につながる、一手順前の図形が何か? と逆から考えると、選択肢を3つまで減らすことが出来ました。
ここから順々にさかのぼって考えていきます。
選択しとなる3つの図形の内、全体の平行四辺形と結びつけやすい図形はどれだろう? と考えます。
下の画像をご覧ください。
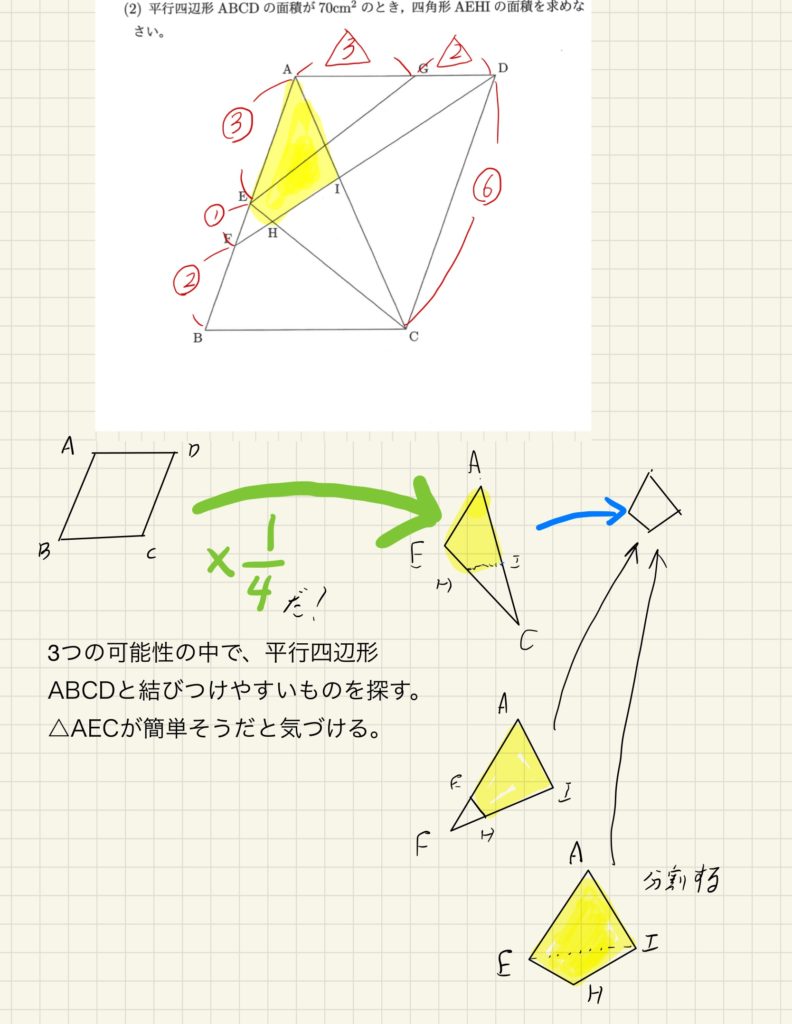
すると、△AEFが全体の平行四辺形ABCDの1/4であることが分かると思います。きっとこれが一番簡単そうなので、この路線で考えることにします。
ここで全体の方針が決まりました。
平行四辺形ABCD→△AEC→四角形AEHI(黄色マーカーの図形) という流れで面積の変化を追っていくことを考えればよいことが分かりました!
下の画像をご覧ください。
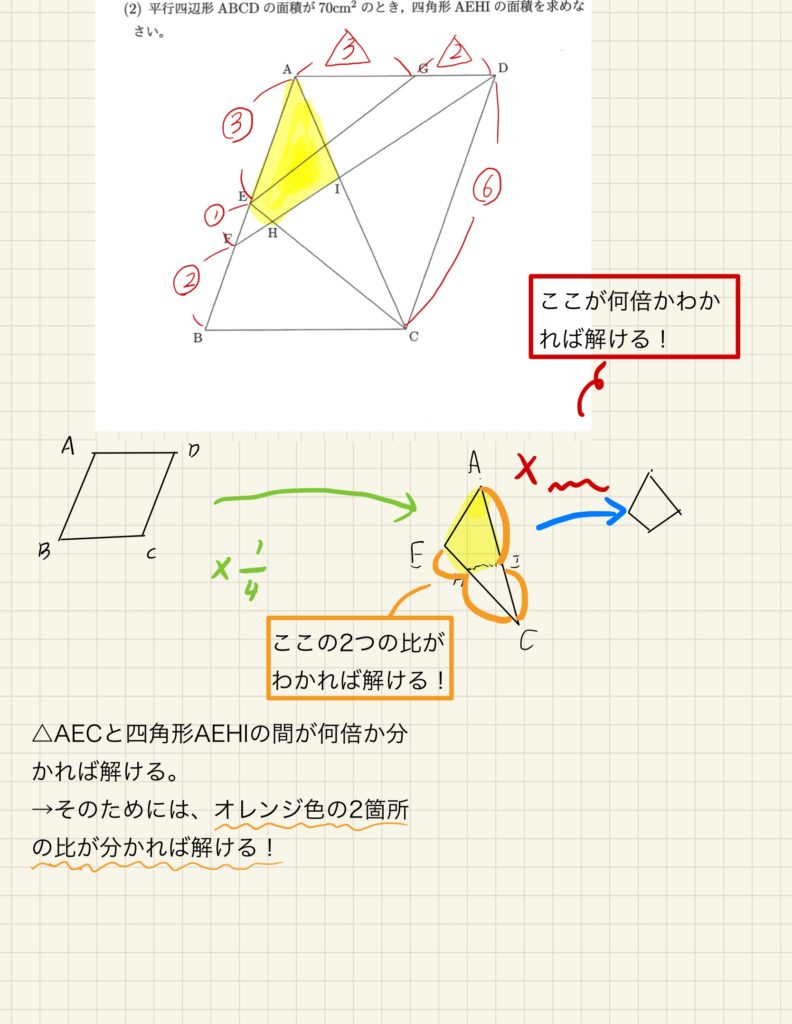
平行四辺ABCD→△AECは1/4倍だと分かっていますので、後は△AEC→四角形AEHIが何倍かが分かれば答えが求まります。
ではそのためには何が分かれば求められるのか? と考えると、AE:ECの比とAI:ICの比(画像内のオレンジ色の比)が分かれば求められることに気づきます。
ここで全ての線がつながりました。
後は、AE:ECの比とAI:ICの比を求めればよいので、相似に着目して比を求めていきます!
ここまでが「解説冊子の0行目」です。
通常の解説は、私がここまで行った解説の次から始まります。つまり
「△EFHと△DICの相似から、EI:HCが1:6だと分かる。また、△AFIと△DICの相似からAI:ICが2:3だと分かる。よって~」
のように書かれています。この記事で画像を5枚使って延々と解説してきた末にたどり着いた「そうか!AE:ECの比とAI:ICを求めれば答えが分かるんだ!」という結論の部分から解説が始まっています。
これでは結果論をなぞっているだけであり、できない子が出来るようになる解説ではありません。
こうした一般的な解説を見た生徒の「なんで突然そこの相似に注目して、そこの比を出そうと思ったの?」という疑問に対する算田なりの解答が今回の記事です。
解けている人が、正解に至る道筋として2つの比に着目するまでには、背景となる思考があるのです。
決してセンスと勘で突然思いついているわけではなく、ゴールから逆算する思考を使って、何を求めるべきかを考えているから着眼すべきポイントに気づけるのです。
算数の家庭教師として個別指導をする際に最も意識しているのがこうした考え方です。
結果論の後付け解説ではなく、生徒が一人で着眼点に気づけるようになるためのトレーニングです。
算田が算数指導で目指しているものはこんな感じのものです。
「教わったから解ける」ではなく「教わった考え方を使ったら自分で解けた」が理想の形です。
ご家庭での指導の際や、また同業の先生で参考にしていただける部分がありましたら是非お使いください。