新シリーズ【算数が得意な人には何が見えているのか】をはじめます。
このシリーズでは、算数が得意な人の頭の中を徹底解剖していきます。
算数が得意な子は一瞬で見てることが、苦手な子は何時間かかっても見えない。
この違いは何なのか?
生まれつきのセンス? 努力では埋められないの?
算数が得意な子が無意識にやっていることを手順に分解することで、誰でも出来るようにしたい!というのが算田の究極の目的です。
算数の能力は、ある程度まではセンスは関係ありません。
出来る人が無意識にやっていることをを努力で埋めてやろう! という企画です。
さっそく始めていきましょう。
第一回はグラフの読み方です。
グラフ、読める人は一瞬で読むんですよね。なんだか天性の閃きがあるみたいです。
グラフの何が困るって、まずどこに注目したら良いのか分からないところです。
なのに!テキストの解答冊子は「ここに注目します。すると~がわかります」から始まっているんです。
そこや……そこの1行目の「ここに注目します」が分からんのや! と思ったことありませんか? 私はあります!ありますよ!!!
天才たちは、何をもって一瞬で「ここに注目だ!」と見抜いているのか。
その秘密を解剖して、誰でも閃けるようにしていきましょう。
手順①グラフで注目するのは「出来事ポイント」だけ
さっそく例題を出してみましょう。容器に水を入れる問題です。
問題:下の図のような容器の★印のところに一定の勢いで水を入れました。グラフは、水を入れ始めてからの時間と、★の部分の深さの関係を表したものです。
1分間に何㎤の水を入れているか答えなさい。
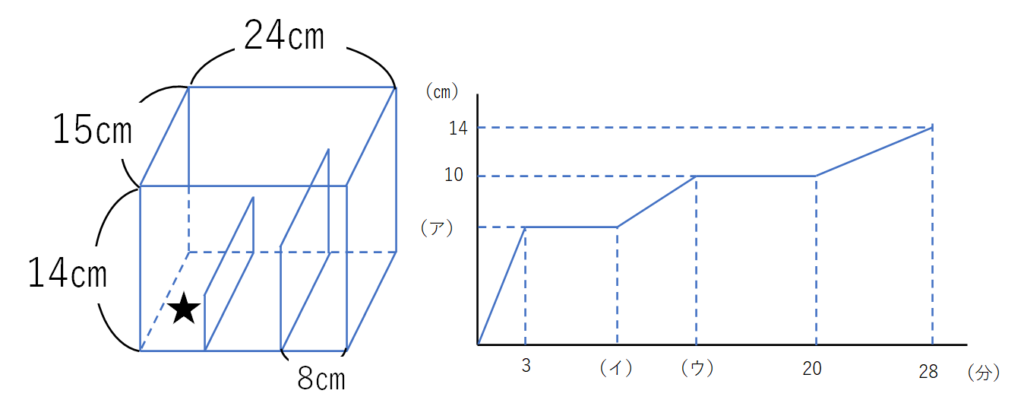
「何を見て何を探せばよいのか」が分かれば問題の8割は解決しています。
算数の問題でも、一般社会の問題でも同じだと思います。
世の中大体そうです。何が問題なのか正確に特定できれば、解けたも同然です。
手順1は「出来事ポイントを探す」
グラフの線が折れ曲がっているところでは、必ず何かの変化・出来事が起きています。
まずグラフの問題を見たら、下の赤字ような書き込みをするようにしましょう。
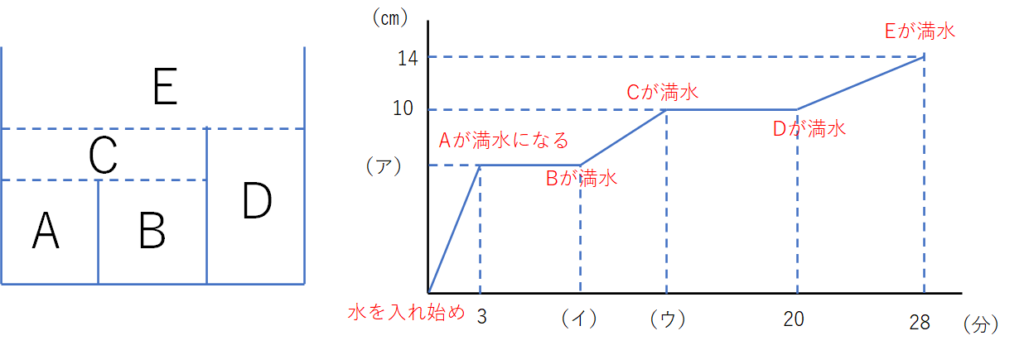
上の図のように、グラフの折れているところで、何が起きているのか、その出来事を簡単に書き込みましょう。
この問題であれば、出来事ポイントは6つです。
このグラフで見るべき場所はこの6点だけです。他の所は見る必要がありません。意味があるのはほぼこの6点だけです。
グラフが苦手な子が悩んでいる際の目線の様子などを観察していると、ぼんやりとグラフ全体を眺めていることが多いです。
どこに注目したらよいのか分からず、全体に平等に注意力を注いでいます。
一方でグラフが得意な子は、この「出来事ポイント」だけを見て検討しています。グラフが折れているポイントだけに絞って検討しているので閃きやすいのです。
こういったところに、得意な子と苦手な子の差があります。
ポイント
出来事ポイントに注目する
さらに深堀りしていきましょう。
「出来事ポイント」はタテとヨコの2つの情報を持っている
グラフ上にある線が折れている点、通称「出来事ポイント」は、2つの情報を持っています。グラフのタテとヨコの数値です。
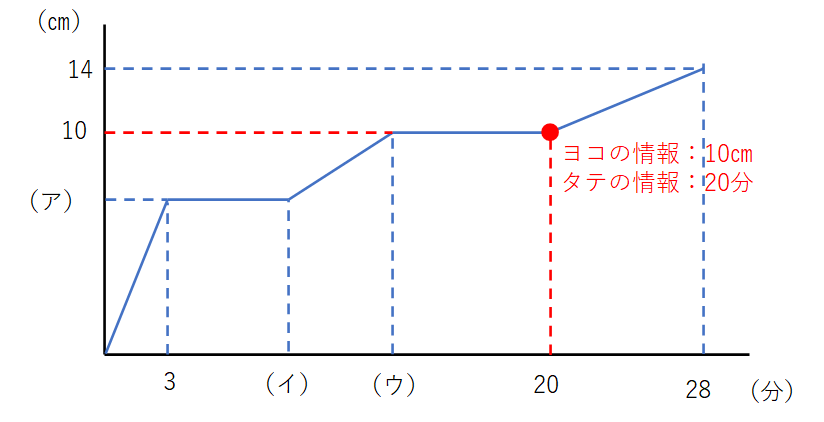
図のように、例えば赤い〇印の点は、10㎝と20分という2つの情報を持っています。
グラフ上の点は、タテとヨコの2つの情報を持っています。言われてみれば当たり前ですが、これがグラフの本質です。
このグラフの6つある出来事ポイントを、情報量によって3つに分類していきましょう。
手順②強い点2つを結ぶ
見るべきポイントは6つに絞れました。ここから更に何を探していけば良いのでしょうか。
結論から言うと「強い点を2つ見つけて結ぶ」です。順に説明していきます。
前の段落でも説明したように、グラフ上の点は2つの情報を持っています。
そんなグラフ上の点にも、強弱があります。「最強の点」「それほど強くない点」「弱い点」と名付けて3つに分類しています。
その点が持っている情報の数によって決まります。
タテとヨコの両方とも分かっている点が「最強の点」
タテか横のどちらか一方だけが分かっている点が「それほど強くない点」
どちらも分かっていない点が「弱い点」です。
下の図を見てください。

グラフ上の点が3種類に分類できました。
問題を解いていくときに、まず最初に見るべきなのは「最強の点」です。
情報がそろっているので、まずはここを足掛かりにするのが正しい第一歩です。
具体的には「最強の点」を2つ見つけて、その2つを結んで考えます。
最強の点を2つ集めると、4つの情報がそろいます。これは強いです。
先ほどの図で試してみましょう。
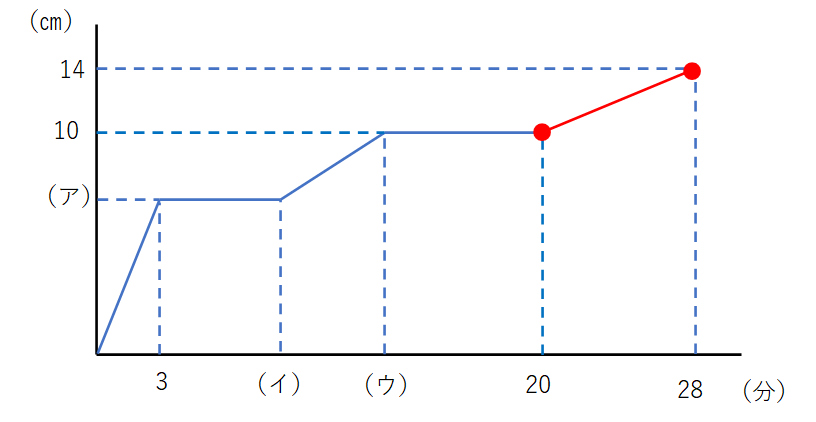
上の図で赤い〇の2か所が最強の点です。この2点を結んだ赤い線が、最も情報がたくさん分かっている区間です。
つまりこの2点を結んで考えると、何か良いことが起きるのでは? というのが方針になります。
手順③あとは解くだけ
さぁ、注目すべきポイントが分かってしまえばあとは解くだけです。
注目した2つの点の間は、図のE区間に水が入っているところです。
つまり、このE区間は28-20=8 の8分で、14-10=4 の4㎝水が上がったということです。もう大丈夫ですね。
15×24×4÷8=180 答え 1分間に180㎤
まとめ
算数が出来る人は何が見えているのか? の答えは手順①と手順②で説明してきました。
ポイント
手順①見るべき場所:線が折れ曲がっている所。通称「出来事ポイント」で何が起きているのか特定する。
手順②探すべきもの:情報が2つとも分かっている点。通称「最強の点」を見つける。
基本はこの2手順のみです。簡単に思えませんか? 水のグラフでも速さのグラフでも、本質はこの2手順です。
グラフの折れている点で何が起きているのかを把握すること。
情報が多く分かっている2点に注目して考えていくこと。
極論すればこの2つで相当数の問題を攻略することが出来ます。
闇雲に勉強するのではなく、問題の本質をとらえた理論に基づいて指導・解説していけば、必ず力はつきます。
ただ一問一問をバラバラに勉強するのではなく、その根底に流れる発想の源泉をかみ砕いて教えてあげたいと思います。
指導者の実力の差は、どれだけ広範囲に適用できる本質的な理論を構築できるかにかかっています。
今後このブログでは、私が持っているとっておきの理論を、文字で伝えられる範囲で全て公開します。